UMA ANÁLISE DA qualidade e DA produtividade de programas de pós-graduação em engenharia

João Carlos Correia Baptista Soares de Mello

Departamento de Engenharia de Produção – Universidade Federal Fluminense

Rua Passo da Pátria 156, 24210-240, Niterói, RJ

gmajcsm@vm.uff.br

Eliane Gonçalves Gomes

Programa de Engenharia de Produção – Universidade Federal do Rio de Janeiro

Caixa Postal: 8183, 21032-970, Rio de Janeiro, RJ

eggomes@pep.ufrj.br

Lidia Angulo Meza

Departamento de Ciências Exatas e Tecnológicas – Universidade Veiga de Almeida

Rua Ibituruna 108, 4º andar, 20271-020, Rio de Janeiro, RJ

lidia_a_meza@yahoo.com

Maria Helena Campos Soares de Mello

Departamento de Engenharia de Produção – Universidade Federal Fluminense

Rua Passo da Pátria 156, 24210-240, Niterói, RJ

mhelenamello@netscape.net

Resumo

Os cursos de pós-graduação são avaliados periodicamente pela CAPES (Coordenação de Aperfeiçoamento de Pessoal de Ensino Superior) segundo critérios nem sempre claros. Esses critérios buscam medir, dentre outros, a produtividade acadêmica (incluindo-se qualidade e quantidade da produção científica), a dedicação do corpo docente, o tempo para conclusão do curso etc. A quantificação da excelência acadêmica não é geralmente realizada; é feita de forma qualitativa. Este artigo tem como objetivo avaliar o desempenho de programas de pós-graduação em Engenharia na capacidade de transformar teses de mestrado e doutorado em produção científica pública, e a produção de cada programa de pós-graduação em relação aos recursos de que dispõe. Para ambos os casos são utilizados modelos de Análise Envoltória de Dados (Data Envelopment Analysis – DEA) com retornos constantes de escala (CCR). São usados como unidades de avaliação os 12 programas de pós-graduação em Engenharia da COPPE (UFRJ).

Palavras-chave: Qualidade, Produtividade, Pós-graduação.

1. Introdução

As avaliações de produtividade em educação são normalmente subjetivas devido à grande quantidade de variáveis a serem consideradas. Para quantificar e agregar essas variáveis em um único índice há a necessidade da imposição de pesos, cuja subjetividade pode ser causa de desconforto e não aceitação dos resultados.

A avaliação educacional deve ser quantitativa e comparada (Boclin, 1999). A abordagem por Análise Envoltória de Dados (Data Envelopment Analysis – DEA) (Cooper et al., 2000) apresenta essas duas características em consonância. No entanto, os pesos atribuídos pelos modelos DEA clássicos são calculados através de um problema de programação linear, de forma que cada DMU se beneficie com a melhor combinação de pesos, maximizando sua eficiência. Entretanto, os pesos podem não ser considerados realistas pelos especialistas no assunto, o que pode gerar dificuldades na aceitação dos resultados do modelo.

É assim desejável uma metodologia que alie a subjetividade da avaliação qualitativa com a objetividade da avaliação quantitativa de DEA (Soares de Mello et al., 2001) [13]. Este artigo, que estende os resultados obtidos por Soares de Mello et al. (2002) [10], tem duplo objetivo: avaliar a eficiência dos Programas de Pós-Graduação em Engenharia da Universidade Federal do Rio de Janeiro em relação à geração de produção científica a partir das teses defendidas e avaliar a produtividade dos seus programas. A primeira medida pode ser encarada como uma medida de qualidade e a segunda como uma medida de produção. Em ambos os casos, são usados modelos DEA com retornos constantes de escala (DEA CCR). No primeiro caso, no qual há um consenso sobre a importância de cada variável, foi utilizada uma técnica de restrição aos pesos. No segundo caso, em que esse consenso não existe, foi usada uma técnica de seleção de variáveis para melhorar a discriminação do modelo.

2. Análise Envoltória de Dados – DEA

A Análise Envoltória de Dados (Data Envelopment Analysis – DEA), desenvolvida originalmente por Charnes et al. (1978) no contexto da avaliação de escolas, é um método que usa programação linear para determinação de eficiências comparativas de Unidades de Tomada de Decisão (Decision Making Units – DMUs) onde não seja preponderante ou não se deseja considerar somente o aspecto financeiro (Gomes et al., 2001). A eficiência relativa de uma DMU é definida como a razão da soma ponderada de seus produtos (outputs) pela soma ponderada dos insumos necessários para gerá-los (inputs).

Ao contrário dos modelos tradicionais de apoio à decisão com vários critérios, não há a figura de um decisor arbitrário que escolhe os pesos para cada fator de ponderação. Eles são obtidos pelo próprio modelo matemático. Para isso, é resolvido um problema de programação fracionária que atribui a cada DMU os pesos que maximizam a sua eficiência. Assim, os pesos são diferentes para cada unidade em estudo e o mais benevolentes possíveis para essa unidade. Portanto, a abordagem por DEA impede que os responsáveis por uma unidade cuja avaliação não tenha sido boa argumentem que tal situação se deveu a uma escolha casuística de pesos.

Os modelos DEA podem levar em conta as diferentes escala de operação. Quando isso acontece o modelo é chamado de BCC (Banker et al., 1984). Quando a eficiência é medida sem considerar os efeitos de escala, o modelo é conhecido como modelo CCR (Charnes et al., 1978). É apresentada em (1) a formulação do problema de programação fracionária, previamente linearizado, para o modelo DEA CCR (Lins e Angulo-Meza, 2000, Cooper et al., 2000).

Para o modelo (1) com n DMUs, m inputs e s outputs, h_o é a eficiência da DMU o em análise; x_ik representa o input i da DMU_k, y_jk representa o output j da DMU k; v_i é o peso atribuído ao input i, u_j é o peso atribuído ao output j. Esse modelo deve ser resolvido para cada DMU.

Neste trabalho foi usado o modelo CCR. A escolha desse modelo é justificada pelo fato de os programas de pós-graduação terem porte semelhante, ou seja, os efeitos relacionados à escala de cada programa não são relevantes.

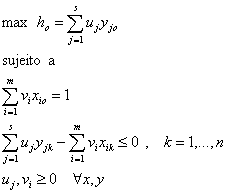
(1)

A estrutura matemática dos modelos DEA faz com que, freqüentemente, uma DMU seja considerada eficiente por serem atribuídos pesos nulos a algumas variáveis. Essas variáveis são desconsideradas na avaliação da eficiência daquela unidade, podendo acarretar uma avaliação incompleta. Essa situação é mais grave quando o número de DMUs é pequeno com relação ao número de variáveis.

Existem duas formas de se contornar essa situação. A primeira utiliza restrições que permitem variar os pesos em certas faixas pré-definidas, minimizando-se a quantidade de variáveis que recebem peso zero (Lins e Angulo-Meza, 2000). A segunda é, dentre todos os possíveis inputs e outputs, escolher os mais relevantes de acordo com critérios quantitativos.

O método de restrição aos pesos compara a “importância” de pares de variáveis, desde que se faça uma prévia normalização para que os pesos retratem fielmente as preferências dos especialistas. Já a seleção de variáveis deve cumprir dois objetivos conflitantes: o ajuste à fronteira e a discriminação completa das DMUs.

O método de restrição aos pesos é utilizado na análise da qualidade e o de seleção de variáveis na análise de produtividade.

3. Avaliação de qualidade e de produtividade dos Programas de Pós-Graduação em Engenharia da Universidade Federal do Rio de Janeiro

3.1. Unidades de avaliação – DMUs

Para este estudo de caso foram selecionados os Programas de Pós-Graduação em Engenharia, sob coordenação do Instituto Alberto Luiz Coimbra de Pós-Graduação e Pesquisa de Engenharia (COPPE), com sede na Universidade Federal do Rio de Janeiro.

A COPPE é constituída de 12 Programas: Engenharia Biomédica (PEB), Engenharia Civil (PEC), Engenharia Elétrica (PEL), Engenharia Mecânica (PEM), Engenharia de Materiais e Metalúrgica (PEMM), Engenharia Nuclear (PEN), Engenharia Naval e Oceânica (PENO), Engenharia de Produção (PEP), Engenharia Química (PEQ), Engenharia de Sistemas e Computação (PESC), Engenharia de Transportes (PET) e Planejamento Energético (PPE). Esses programas representam as DMUs do modelo DEA.

3.2. Avaliação de qualidade

Para a avaliação da qualidade científica, as variáveis selecionadas representam as teses publicadas e as publicações provenientes dessas teses. Como recursos (inputs) foram escolhidas as Teses de Mestrado (TM) e as Teses de Doutorado (TD); como produtos (outputs), as publicações em Revistas Internacionais (RI), em Revistas Nacionais (RN), em Congressos Internacionais (CI) e Nacionais (CN), Livros publicados (L) e Extras (EX). Este modelo mede a capacidade de cada programa de gerar publicações científicas baseadas nas teses defendidas.

Os dados utilizados referem-se ao somatório das variáveis para o período compreendido entre 1996 e 2000 (inclusive). O uso deste intervalo temporal alargado tem como objetivo diluir a defasagem entre a data da defesa das teses e a data de publicação de seus resultados para a comunidade científica.

Assim, o modelo DEA CCR é constituído de 12 DMUs, 2 inputs e 6 outputs. A Tabela 1 apresenta os valores das variáveis.

Tabela 1 - Valores para as variáveis.

DMUs	TM	TD	RI	RN	CI	CN	L	EX
PEB	59	24	24	21	66	194	0	6
PEC	189	88	71	22	283	186	3	28
PEL	132	33	83	13	229	165	2	16
PEM	79	30	60	13	81	136	1	9
PEMM	114	47	107	29	102	277	1	4
PEN	62	29	46	10	50	131	0	1
PENO	72	19	17	5	71	62	0	19
PEP	286	181	22	44	66	179	8	53
PEQ	79	69	139	32	138	332	1	6
PESC	150	78	62	22	183	211	3	92
PET	72	15	7	12	57	91	2	33
PPE	84	4	12	13	31	41	7	32

3.2.1. Modelo DEA CCR sem restrições aos pesos

As Tabelas 2 e 3 mostram, respectivamente, os resultados de eficiência e as DMUs de referência (ou benchmarks) para as ineficientes, e os pesos atribuídos pelo modelo para as variáveis.

Cabe destacar que para as DMUs eficientes os pesos apresentados não são únicos, ou seja, para tais DMUs outro software utilizado pode encontrar um conjunto diferente de pesos que mantenha a DMU com eficiência 100%.

Como pode ser observado na Tabela 3, existem de três a cinco pesos nulos para cada DMU, o que significa que essas variáveis estão sendo desconsideradas como critérios de avaliação. Ou seja, um grande número de critérios julgados importantes na avaliação não foram levados em conta. Assim, torna-se necessário um refinamento do modelo usado.

Tabela 2 - Eficiências no modelo DEA CCR, sem restrições aos pesos.

DMUs	Eficiência (%)
PEB	100,0
PEC	90,6
PEL	100,0
PEM	89,0
PEMM	100,0
PEN	76,8
PENO	79,2
PEP	61,5
PEQ	100,0
PESC	100,0
PET	100,0
PPE	100,0

Tabela 3 - Pesos atribuídos no modelo DEA CCR sem restrições.

DMUs	Pesos
	TM	TD	RI	RN	CI	CN	L	EX
PEB	2,144	4,206	0,000	1,570	0,000	0,429	0,000	0,000
PEC	1,513	0,000	0,000	0,027	0,782	0,000	0,366	0,219
PEL	0,614	3,930	0,305	0,000	1,010	0,000	0,000	0,000
PEM	0,876	4,574	1,986	0,000	0,000	0,207	0,000	0,591
PEMM	0,284	3,415	0,655	0,068	0,000	0,540	0,000	0,000
PEN	1,170	4,659	1,087	0,000	0,603	1,353	0,000	0,000
PENO	2,654	3,163	0,000	0,000	2,398	0,000	0,000	1,930
PEP	1,000	0,000	0,000	0,544	0,000	0,000	0,154	0,523
PEQ	3,620	0,000	0,756	0,000	0,450	0,000	0,000	0,372
PESC	1,907	0,000	0,301	0,000	0,000	0,000	0,000	0,866
PET	2,543	4,342	0,000	0,000	1,188	0,996	0,000	1,359
PPE	0,000	45,250	0,000	0,000	0,000	0,000	1,143	0,000

3.2.2. Modelo DEA CCR com restrições aos pesos

Na avaliação do item anterior não foi possível obter uma boa ordenação das DMUs, isto é, verifica-se a existência de uma grande quantidade de unidades 100% eficientes. Tal fato é uma característica dos modelos DEA clássicos e ocorre quando o número de variáveis é muito superior ao número de DMUs. Existe uma recomendação empírica de que o número de DMUs deve ser pelo menos o triplo do número de variáveis. No presente estudo essa relação não é verificada, o que gera a grande quantidade de DMUs eficientes.

A necessidade de obter uma melhor ordenação e a indesejável existência de múltiplos pesos nulos, recomendam a inclusão de restrições aos pesos no modelo. Existem duas formas clássicas de fazer essa restrição. A primeira é indicar percentuais de importância de cada variável (Soares de Mello et al., 2001; Soares de Mello et al., 2002) [13, 11]. Embora evite completamente o problema da existência de pesos nulos, essa abordagem obriga a que o decisor dê uma informação bastante completa, nem sempre consensual.

Uma outra abordagem pede apenas que o decisor indique uma ordenação de importância entre os inputs e outputs considerados. Embora essa abordagem ainda permita a existência de pesos nulos, os julgamentos de valor emitidos são, normalmente, consensuais. Foi então adotada esta abordagem, com os seguintes julgamentos de valor: para a produtividade científica, as publicações em revista são mais relevantes que as publicações em congresso; as publicações internacionais são preferíveis às publicações nacionais; todos os tipos de publicação são mais relevantes que as publicações classificadas como extras; a publicação em revista internacional é mais importante que livros. Com relação aos inputs, considera-se que as teses de doutorado, pela necessidade de ineditismo teórico, são consideradas mais relevantes que as de mestrado.

Para a correta aplicação dos pesos, os dados correspondentes às variáveis foram normalizados. Com a aplicação do modelo DEA CCR com restrições aos pesos, foram obtidos os resultados da Tabela 4, na qual apresentam-se os pesos e a eficiência de cada DMU.

Tabela 4 - Resultados do modelo DEA CCR, com restrições aos pesos.

DMUs	Eficiência (%)	Pesos
		TM	TD	RI	RN	CI	CN	L	EX
PEB	100,0	2,122	4,240	0,670	0,670	0,670	0,670	0,249	0,249
PEC	63,5	0,900	0,833	0,360	0,000	0,360	0,000	0,242	0,000
PEL	100,0	1,500	1,688	0,711	0,000	0,711	0,000	0,000	0,000
PEM	87,5	0,865	4,592	1,952	0,000	0,022	0,000	0,211	0,000
PEMM	100,0	0,759	2,685	0,502	0,337	0,320	0,320	0,053	0,053
PEN	72,4	1,259	4,538	0,854	0,546	0,576	0,546	0,000	0,000
PENO	55,5	1,895	4,982	0,842	0,657	0,842	0,657	0,185	0,185
PEP	36,0	0,690	0,310	0,167	0,167	0,000	0,000	0,167	0,000
PEQ	100,0	3,620	0,000	0,294	0,294	0,294	0,294	0,294	0,294
PESC	70,6	1,158	0,912	0,196	0,196	0,196	0,196	0,196	0,196
PET	77,6	2,396	4,788	0,757	0,757	0,757	0,757	0,281	0,281
PPE	100,0	3,287	1,569	0,934	0,000	0,934	0,000	0,934	0,000

Comparando-se as Tabelas 2, 3 e 4, observa-se uma redução no número de DMUs eficientes, de sete para cinco, como resultado da inclusão das restrições aos pesos. O número de pesos nulos passou a variar de zero a três. Conseguiu-se uma melhor ordenação das DMUs e uma avaliação mais completa por não desconsiderar um menor número de variáveis.

3.2.3. Análise de resultados

Uma comparação dos dois modelos revela que as DMUs PESC e PET deixaram de ser eficientes quando da aplicação do modelo com restrições aos pesos. Isto indica que no modelo inicial, estas DMUs eram eficientes devido a uma combinação muito particular de pesos.

Já as DMUs PEB, PEL, PEMM, PEQ e PPE são eficientes em ambos os modelos. Esta situação indica uma robustez na eficiência. É interessante observar que dentre estas cinco DMUs, encontram-se as únicas com conceito máximo na avaliação realizada pela Coordenação de Aperfeiçoamento de Pessoal de Ensino Superior – CAPES (PEQ e PEMM).

Já a DMU PEP teve a mais baixa eficiência em ambos os modelos. Isto sugere falta de empenho ou falta de possibilidade em divulgar os resultados obtidos na teses defendidas. Ao comparar-se, em especial, o resultado de sua eficiência no modelo com restrições aos pesos (36%) com o resultado da segunda mais baixa eficiência (55,5%), nota-se a discrepância entre os resultados das publicações do PEP com os dos outros programas avaliados. Destaca-se, ainda, que a eficiência 36% do PEP foi conseguida com três pesos nulos, ou seja, desconsiderando-se três critérios de avaliação.

Ainda sobre o PEP é interessante observar a necessidade de uma definição de estratégia para publicações. Apesar de esta DMU ter um bom número de publicações em congressos nacionais, o modelo atribuiu peso nulo a essa variável. De fato, as restrições impostas obrigam a que o peso para os congressos internacionais seja, pelo menos, igual ao dos congressos nacionais. Assim, a falta de participação em congressos internacionais obriga a que o modelo DEA ignore a boa participação do PEP em congressos nacionais, para não ser penalizado pela falta de participação em congressos internacionais.

3.3. Avaliação de produtividade

A modelagem usada na avaliação da produtividade é semelhantes à utilizada em Angulo-Meza (1998), Angulo-Meza e Lins (1999) e Lins e Angulo-Meza (2000) para determinação da eficiência Programas de Pós-Graduação de Engenharia da Universidade Federal do Rio de Janeiro, no qual o problema da baixa discriminação foi resolvido pelo uso de Avaliação Cruzada. Neste artigo, ao invés da avaliação cruzada, é utilizado o método da escolha seletiva de variáveis.

Os inputs usados no modelo DEA estão relacionados aos recursos humanos utilizados por cada programa: número total de professores (PROF); número total de funcionários (FUNC). Os outputs refletem as diversas atividades desenvolvidas em ensino, pesquisa e extensão: valores totais (em reais) dos projetos (PROJ); publicações científicas, agregadas segundo um índice criado pela Comissão de Avaliação de Docentes da universidade (PUB); teses de mestrado (MEST) e de doutorado (DOC) defendidas; aulas ministradas (AULA).

Devido ao grande número de variáveis e à falta de consenso para impor restrições aos pesos torna-se necessário escolher apenas quatro variáveis para compor o modelo. A escolha dessas variáveis é feita segundo a abordagem proposta por Soares de Mello et al. (2001) [12], que faz uso de um modelo multicritério para a escolha de variáveis a serem incorporadas ao modelo DEA. Esta abordagem permite uma boa ordenação, sem grande prejuízo ao ajuste das DMUs à fronteira de eficiência e mostra-se útil principalmente em casos de avaliação de eficiência em que seja necessário o uso de um pequeno número de DMUs e haja disponibilidade de um grande número de variáveis (inputs e outputs).

A aplicação do método conduz à utilização das seguintes variáveis. Os inputs usados no modelo DEA estão relacionados aos recursos humanos utilizados por cada programa: número total de professores (PROF). Os outputs refletem as diversas atividades desenvolvidas em ensino, pesquisa e extensão: valores totais (em reais) dos projetos (PROJ); publicações científicas, agregadas segundo um índice criado pela Comissão de Avaliação de Docentes da universidade (PUB); teses de mestrado (MEST). Os resultados são apresentados na Tabela 5.

3.4. Eficiência geral

Observando os resultados obtidos em ambos os modelos, nota-se que a DMU PEQ foi a única que resultou eficiente nas duas abordagens.

É interessante que haja uma medida de eficiência que agregue a produtividade e a qualidade de forma que um programa só seja considerado eficiente se for simultaneamente produtivo e de qualidade. Uma forma de se fazer isso é agregando os dois índices de eficiência em um índice agregado, resultado do produto dos dois anteriores. Esta é considerada uma abordagem agressiva. Uma outra abordagem é um novo modelo DEA, em que o input é a próprio existência da DMU (constante igual a 1) e os ouputs são as eficiências dos modelos anteriores. Esta abordagem é considerada benevolente, já que nela basta ser eficiência em uma das eficiências parciais para ser eficiente no índice agregado final. A Tabela 6 apresenta os resultados das duas abordagens.

Tabela 5 - Resultados de eficiência para o modelo.

DMU	Eficiência (%)
PEB	91,5
PEC	75,6
PEL	79,4
PEM	46,5
PEMM	59,8
PEN	74,6
PENO	72,5
PEP	79,6
PEQ	100,0
PESC	84,3
PET	100,0
PPE	84,2

Tabela 6 - Resultados da eficiência geral.

DMUs	Eficiência Geral (%) agressiva	Eficiência Geral (%) benevolente
PEQ	100,0	100,0
PEB	91,5	100,0
PPE	84,2	100,0
PEL	79,4	100,0
PET	77,6	100,0
PEMM	59,8	100,0
PESC	59,5	84,3
PEN	54,0	74,6
PEC	48,0	75,6
PEM	40,7	87,5
PENO	40,3	72,5
PEP	28,7	79,6

O índice de eficiência agregado agressivo ratifica as conclusões já obtidas nos modelos anteriores, em especial no que se refere às DMUs PEQ e PEP, que apresentam o melhor e o pior desempenho geral, respectivamente. O PEQ, pelo fato de ser eficiente nas duas avaliações teria que ter eficiência máxima no índice agregado. Já o PEP, embora tenha uma eficiência mediana em produtividade, acaba tendo um péssimo resultado geral devido à avaliação de qualidade.

O índice de eficiência agregado benevolente não permite grandes análises devido ao elevado número de DMUs com eficiência 100%. Cabe ressaltar que nesta agregação o PEP deixou de ter o pior índice, que passou a ser do PENO. Nas análises posteriores serão levados em consideração os resultados do índice agregado agressivo.

É interessante uma análise do PEMM, que tem conceito 7 na avaliação CAPES. Este programa, na avaliação aqui efetuada foi eficiente em qualidade, mas não em produtividade, o que prejudicou a sua avaliação geral. Já o PET, não tão bem avaliado pela CAPES, apresenta-se bem em produtividade, e mal em qualidade. A comparação destes dois resultados sugere que a CAPES tem avaliações distorcidas, por não considerar os meios de cada programa obter os seus resultados. É evidente que essa afirmação necessita ainda de mais testes para passar de suposição a constatação.

4. Conclusões

A Análise Envoltória de Dados mostrou-se uma ferramenta importante para a avaliação da produtividade científica, ao serem consideradas múltiplas variáveis que apresentam relação causal.

Os resultados obtidos independem de opiniões subjetivas, e sempre polêmicas, dos avaliadores, sejam internos, como a CAD (Comissão de Avaliação de Docentes), ou externos, como a CAPES. As únicas opiniões incluídas no modelo de restrições aos pesos, são, geralmente, consensuais na comunidade científica.

A inclusão de restrições aos pesos permite um refinamento do modelo DEA clássico, mantendo, no entanto, grande consistência de resultados em ambos os modelos. Por outro lado, se não tivessem sido consideradas restrições aos pesos, os resultados teriam pouco significado, devido à alta relação variáveis–DMUs. Sempre que essa relação for alta, os resultados só podem ser validados se ao modelo DEA forem incorporadas técnicas adicionais. A técnica de restrições aos pesos é apenas uma destas. O uso seletivo de variáveis, que foi empregue sem grande detalhamento teórico, é outra técnica útil, embora pouco usada na literatura.

É importante ressaltar que os resultados obtidos em DEA são sempre comparativos. Assim, não é necessário (nem sequer possível) comparar os resultados com os obtidos em outros problemas de avaliação. As comparações feitas neste artigo são entre diferentes programas de uma mesma instituição. Em Sant´Anna (2002) é feita uma comparação de programas homônimos em instituição diferentes, e os resultados aí obtidos podem ser considerados uma avaliação complementar à que aqui foi feita.

Os resultados deste artigo podem contribuir no balizamento de políticas de melhoria acadêmica dos programas analisados. Porém, esta avaliação não pretende ser exaustiva, uma vez que existem várias vertentes a serem analisadas.

5. Referências Bibliográficas

[1] Angulo-Meza, L. Data Envelopment Analysis na determinação da eficiência dos Programas de Pós-Graduação da COPPE/UFRJ, Tese (Mestrado em Eng. de Produção) - COPPE, Universidade Federal do Rio de Janeiro, Rio de Janeiro, 1998.

[2] Angulo-Meza, L. & Lins, M.P.E. Incremento da Discriminação na Análise Envoltória de Dados utilizando Avaliação Cruzada e a sua aplicação na determinação da eficiência nos Programas de Pós Graduação da COPPE/UFRJ, Anais do XXXI Simpósio Brasileiro de Pesquisa Operacional, 1999.

[3] Banker, R.D., Charnes, A. & Cooper, W.W. (1984). Some models for estimating technical scale inefficiencies in Data Envelopment Analysis. Management Science, 30, 1078-1092.

[4] Boclin, R. (1999). Indicadores de Desempenho: Novas Estratégias da Educação Superior. Ensaio - Avaliação e Políticas Públicas em Educação, 7, 299-308.

[5] Charnes, A., Cooper, W.W. & Rhodes, E. (1978) Measuring the efficiency of decision-making units. European Journal of Operational Research, 2, 429-444.

[6] Cooper, W.W., Seiford, L.M. & Tone, K. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software, Kluwer Academic Publishers, Boston, 2000.

[7] Gomes, E.G., Soares de Mello, J.C.C.B., Serapião, B.P., Lins, M.P.E. & Biondi, L.N. (2001). Avaliação de Eficiência de Companhias Aéreas Brasileiras: Uma Abordagem por Análise de Envoltória de Dados. In: Setti, J.R.A., Lima Júnior, O.F. (Eds.). Panorama Nacional da Pesquisa em Transportes 2001, 2, 125-133.

[8] Lins, M.P.E. & Angulo-Meza, L. Análise Envoltória de Dados e perspectivas de integração no ambiente de Apoio à Decisão. Editora da COPPE, Rio de Janeiro, 2000.

[9] Sant’Anna, A.P. Modelagem e Avaliação de Produtividade de Cursos de Mestrado em Engenharia de Produção. Anais do XXII Encontro Nacional de Engenharia de Produção, 2002.

[10] Soares de Mello, J.C.C.B., Gomes, E.G., Angulo-Meza, L. & Soares de Mello, M.H.C. Medida de Relevância e Visibilidade das Teses de Programas de Pós-Graduação em Engenharia. Anais do XXX Congresso Brasileiro de Ensino de Engenharia, 2002.

[11] Soares de Mello, J.C.C.B., Lins, M.P.E., Soares de Mello, M.H.C. & Gomes, E.G. (2002). Evaluating the Performance of Calculus Classes Using Operational Research Tools. European Journal of Engineering Education, 27 (2), 209-218.

[12] Soares de Mello, J.C.C.B., Gomes, E.G., Soares de Mello, M.H.C. & Lins, M.P.E., Seleção de Variáveis para utilização de Análise Envoltória de Dados como ferramenta Multicritério: uma aplicação em Educação. Anais do XXI Encontro Nacional de Engenharia de Produção e VII International Conference on Industrial Engineering and Operations Management, 2001.

[13] Soares de Mello, J.C.C.B., Leta, F.R., Fernandes, A.J.S., Vaz, M.R., Soares de Mello, M.H.C. & Barbejat, M.E.R.P. (2001) Avaliação Qualitativa e Quantitativa: uma Metodologia de Integração. Ensaio – Avaliação e Políticas Públicas em Educação, 9 (31), 237-251.