ANÁLISE DA PRODUTIVIDADE DO SETOR ODONTOLÓGICO DO SISTEMA DE SAÚDE DA MARINHA UTILIZANDO O ÍNDICE DE MALMQUIST

 

 

Annibal Parracho Sant’Anna

Universidade Federal Fluminense

tppaps@vm.uff.br

 

Cleber Almeida de Oliveira

Centro de Apoio a Sistemas Operativos – Marinha do Brasil

cleberamo@aol.com

 

Marcos Pereira Estellita Lins

Universidade Federal do Rio de Janeiro

estellit@iis.com.br

 

 

RESUMO

 

Este trabalho aplica a Análise Envoltória de Dados (DEA) a dados extraídos dos resumos anuais da Diretoria de Saúde da Marinha do Brasil (DSM). A medida do crescimento da produtividade total dos fatores ao longo do tempo, utilizando o método de Malmquist-DEA complementou a análise dos dados. Esta abordagem permite evidenciar o crescimento da produtividade ao mesmo tempo que identifica as unidades observadas que determinam padrões de referência para esse crescimento.

 

 

ABSTRACT

 

This paper synthesizes the results of a research aimed to exploit the potential of Data Envelopment Analysis (DEA) as a tool for analysis and evaluation of relative productivity of the Brazilian Navy Health System in the dentistry sector from 1996 to 2000. DEA methodology was used to calculate Malmquist indices to measure and follow the Total Factor Productivity (TFP) growth of the evaluated health units along those years.

 

Keywords: Data Envelopment Analysis - Malmquist Index - Productivity

 

 

 

1. INTRODUÇÃO

 

Esta aplicação da Análise Envoltória de Dados (DEA) baseou-se em dados extraídos dos resumos anuais da Diretoria de Saúde da Marinha (DSM) colhidos nos anos de 1996 a 2000 relativos ao setor odontológico das unidades hospitalares DA Marinha do Brasil que assistiam os militares da Força e seus dependentes. O emprego da DEA permitiu realizar diversas comparações dispensando a interferência de especialistas na obtenção de indicadores de performance. A introdução do conceito de produtividade relativa abriu novas alternativas para a avaliação anual da produtividade.

DEA é uma técnica baseada em programação linear para medida da eficiência técnica, desenvolvida e aprimorada por um grande número de autores, tais como Charnes, Cooper e Rhodes (1978), Banker, Charnes e Cooper (1984) e Färe, Grosskopf e Lovell (1985). Na sua essência, os vários modelos da DEA se baseiam na determinação do subconjunto das unidades tomadoras de decisão (DMUs) que fazem parte da superfície envolvente ou fronteira de eficiência dos dados observáveis. A forma geométrica desta superfície envolvente depende do modelo de DEA utilizado. Uma DMU é considerada eficiente se pertencer a essa fronteira. As DMUs que não pertencerem a essa envolvente são caracterizadas como relativamente ineficientes e recebem uma medida de eficiência relativa.

A medida do crescimento da produtividade total dos fatores (Total Factor Productivity – TFP Growth), permitindo acompanhar a evolução da produtividade das unidades avaliadas ao longo dos anos, complementou a análise dos dados. O método de Malmquist-DEA, proposto por Färe, Grosskopf, Norris e Zhang (1994), é o que tem sido mais estudado e aplicado nos últimos anos para cálculo desta medida. Sua popularidade deve-se, principalmente, a duas vantagens que decorrem da aplicação da DEA para identificação da fronteira de eficiência. Estas vantagens são: (i) nenhuma informação de preço é requerida e (ii) as medidas de mudanças de TFP podem ser decompostas em componentes, tais como ‘mudanças na tecnologia’ e ‘mudanças na eficiência técnica’. Um componente novo em nossa análise é a comparação dos resultados obtidos aplicando a proposta de Färe et alii (1994) com a de Bjurek (1996) para avaliar o efeito da hipótese de retornos constantes de escala da DEA no cálculo do índice de Malmquist.

As variáveis que definiram o modelo foram: a média do efetivo de cirurgiões-dentistas e o número de consultórios odontológicos operantes, como fatores de entrada, e o total de consultas, como fator de saída. Com isto se aprimorou a estrutura de análise anteriormente aplicada, que era baseada no cálculo de índices que não levavam em conta a disponibilidade de consultórios nem de cirurgiões-dentistas.

Como ponto de partida, estabelecemos nossos objetivos em termos de maximização dos outputs (quantidades das saídas oferecidas) que poderão ser obtidos sem elevar o nível dos inputs (quantidades das entradas utilizadas). Isto se justifica porque, no setor público, alterações nos insumos não são fáceis e demandam ações externas às organizações hospitalares, de modo que os incrementos na produtividade desses órgãos são buscados através da elevação do volume dos resultados obtidos com a plena utilização dos recursos, fixados em montantes sempre pequenos relativamente à demanda realmente enfrentada. O modelo para a maximização dos outputs tenta encontrar o maior aumento proporcional da produção da DMU em análise, de forma que esta ainda satisfaça suas limitações nos inputs.

Na Seção 2, aplicamos DEA ao conjunto dos dados dos 5 anos. Na Seção 3, discutimos a metodologia aplicada para a análise da evolução da produtividade ao longo do tempo baseada no uso da DEA para o cálculo do índice de Malmquist. Na Seção 4, apresentamos os dados selecionados e aplicamos aos mesmos a metodologia de Malmquist-DEA. Na Seção 5, introduzimos a abordagem de Bjurek (1996) e comparamos os resultados obtidos através desta metodologia com os obtidos anteriormente.

 

 

2. DADOS E PRIMEIROS CÁLCULOS DE EFICIÊNCIA

 

Para tentar evitar que particularidades operacionais comprometessem a homogeneidade do conjunto de DMUs, este estudo se restringe às unidades do Serviço de Saúde da Marinha que assistem os militares e seus dependentes. Isto reduz o conjunto analisado a nove unidades, 3 unidades ambulatoriais no Rio de Janeiro: HCM, OCM, PNNSG e 6 hospitais fora do Rio de Janeiro: HNSA, HNRE, HNNA, HNBE, HNLA, HNBR. A Tabela 2.1 apresenta os valores das variáveis consideradas.

 

 

Tabela 2.1. Variáveis de Entrada e Saída

 

Entradas

Saída

DMU

X 1 - Dentistas

X 2 – Consultorios

Y3 –  Consultas

 

96

97

98

99

00

96

97

98

99

00

96

97

98

99

00

HCM

8

8

8

11

14

12

13

13

13

17

16.980

14.942

12.685

15.262

17.127

HNBE

19

18

18

18

18

12

12

12

12

12

17.168

10.703

9.875

18.348

21.025

HNBR

11

18

22

22

24

8

8

8

8

8

16.420

17.104

12.607

13.761

16.819

HNLA

7

8

9

9

10

4

4

4

4

5

7.874

8.083

14.731

13.505

14.332

HNNA

10

11

10

11

13

8

8

8

8

8

15.987

10.062

11.438

13.381

18.448

HNSA

13

16

16

15

20

10

10

11

11

11

18.834

18.810

14.842

17.049

26.420

HNRE

8

12

11

10

10

7

6

7

5

4

6.324

14.077

16.341

15.864

21.250

PNNSG

22

23

24

35

38

19

27

27

27

27

35.080

32.849

38.170

44.410

49.907

COM

80

82

87

97

94

64

65

68

68

66

100.216

103.782

104.772

123.032

135.964

 

 

 

            A tabela 2.2 apresenta as correlações entre as variáveis. As correlações entre as duas variáveis de entrada são bastante elevadas significando que recursos humanos especializados e instalações são utilizados em proporções semelhantes. Observam-se, também, correlações elevadas entre as variáveis de entrada e a variável de saída.

 

 

 

Tabela 2.2 – Análise de Correlação entre Variáveis

 

Nº Dentistas

Nº Consultórios

Nº Consultas

 Nº Dentistas

1

 

 

 Nº Consultórios

0,97

1

 

 Nº Consultas 

0,98

0,97

1

 

 

 

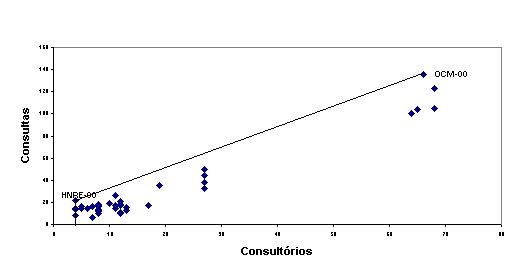
As figuras 2.1 e 2.2 apresentam as eficiências parciais no modelo DEA VRS, em relação a cada um dos inputs, considerando-se os dados coletados, anualmente, de cada unidade hospitalar avaliada. Ao calcularmos a eficiência parcial em relação ao número de dentistas, verificamos (Figura 2.1) que as DMUs HCM-96, OCM-00, HNRE-00 e HNLA-96 pertencem à fronteira de eficiência. No cálculo da eficiência parcial em relação ao número de consultórios, verificamos (Figura 2.2) que as DMUs HNRE-00 e OCM-00 pertencem à fronteira de eficiência.

 

 

Figura 2.1 - Eficiência Parcial em Relação ao Nº de Dentistas

Figura 2.2 - Eficiência Parcial em Relação ao Nº de Consultórios

 

A tabela 2.3 resume os valores de eficiência relativa obtidos nas análises dos modelos CRS para as 9 unidades hospitalares, nos anos de 1996 a 2000.

 

 

Tabela 2.3 – Eficiências no Modelo CRS

ANO

HCM

HNBE

HNBR

HNLA

HNNA

HNSA

HNRE

PNNSG

OCM

1996

100%

69,7%

100%

95,9%

100%

93,2%

49,4%

96,9%

78,4%

1997

100%

46,6%

91,1%

86,1%

69,6%

94,0%

100%

89,9%

93,5%

1998

96,9%

33,5%

42,8%

100%

69,9%

56,7%

90,8%

97,2%

73,6%

1999

89,0%

64,3%

50,9%

100%

76,7%

71,6%

100%

80,0%

80,0%

2000

57,6%

55,0%

39,6%

67,4%

66,8%

62,2%

100%

61,8%

68,1%

 

Quando o aumento de produção é proporcional ao dos inputs, há rendimentos constantes à escala (CRS). Se o aumento dos outputs for superior ao aumento proporcional, há rendimentos crescentes à escala (IRS) e, se o aumento for inferior, há rendimentos decrescentes à escala (DRS). O tipo de rendimento à escala fica determinado no modelo CRS pelo somatório dos pesos das unidades de referência (Banker e Thrall, 1992): se a soma dos l for maior que 1 para todas as soluções ótimas alternativas, então prevalecem rendimentos decrescentes à escala (DRS) no ponto projetado da DMUk; se for menor que 1 para todas as soluções ótimas alternativas, então prevalecem rendimentos crescentes à escala (IRS) no ponto projetado da DMUk; se for igual a 1 para alguma dessas soluções, então prevalecem rendimentos constantes à escala (CRS) no ponto projetado da DMUk.

No modelo VRS, o rendimento à escala é determinado pelo coeficiente linear do hiperplano suporte da unidade avaliada (Banker et alii, 1984). Banker e Thrall (1992) mostraram que o sinal de  é igual ao sinal de , quando a eficiência medida pelo modelo CRS for menor que 1.

 

Tabela 2.4. Somatório dos Lambdas

DMU

1996

1997

1998

1999

2000

HCM

1

1

0,89

1,1

1,4

HNBE

1,5

1,61

2

1,8

1,8

HNBR

1

1,33

2

2

2

HNLA

0,5

0,67

1

1

1

HNNA

1

1,01

1,11

1,1

1,3

HNSA

1,25

1,41

1,78

1,5

2

HNRE

0,82

1

1,22

1

1

PNNSG

2,25

2,49

2,67

3,5

3,8

OCM

8

7,73

9,67

9,7

9,4

 

 

A Tabela 2.4 sugere que algumas unidades operam em faixa de rendimentos decrescentes de escala, sobretudo as duas unidades de maiores dimensões. Rendimentos decrescentes de escala podem ocorrer devido às unidades maiores realizarem procedimentos de maior complexidade ou possuírem mais funções de administração geral, a serem exercidas por cirurgiões-dentistas. A análise dos resultados da DEA, isoladamente, não permite, entretanto, avaliar estes possíveis fatores.         

O caso extremo é o de OCM, que, com dimensões muito maiores que as dos demais hospitais, pode ter sua ineficiência atribuída a rendimentos decrescentes de escala. É o que se verifica, ao aplicar o modelo VRS, que, conforme explicado acima, atribui eficiência 1 a todas as unidades com valores extremos. As eficiências segundo o modelo VRS são mostradas na Tabela 2.5.

 

 

Tabela 2.5. Eficiências no Modelo VRS

ANO

HCM

HNBE

HNBR

HNLA

HNNA

HNSA

HNRE

PNNSG

OCM

1996

100%

74,0%

100%

100%

100%

95,1%

53,7%

100%

100%

1997

100%

48,0%

99,9%

100%

69,7%

96,1%

100%

99,7%

100%

1998

100%

38,8%

61,9%

100%

70,2%

63,1%

91,7%

100%

100%

1999

90,8%

71,3%

65,6%

100%

78,3%

77,4%

100%

95,2%

100%

2000

64,1%

65,3%

58,7%

67,4%

72,8%

77,2%

100%

83,9%

100%

 

Comparando-se os resultados obtidos, verifica-se variação expressiva de um ano para o outro em determinadas unidades hospitalares. Isto pode ter ocorrido por mudança na administração ou forte variação no número de militares destacados em outras organizações militares, em licenças especiais ou em funções administrativas. Pode, também, ser atribuído aos erros de registro. O que mais chama a atenção, entretanto, são as mudanças nos resultados quando se passa da abordagem CRS para a abordagem VRS, principalmente nas unidades que apresentam os dados dos inputs bem acima da média das outras unidades tais como PNNSG e OCM. A Tabela 2.6 aprofunda a análise dessas diferenças. Refere-se ao ano de 2000, mas a análise dos anos anteriores produz resultados similares.

 

 

Tabela 2.6. Pontos projetados e Percentuais das Folgas nos modelos CRS e VRS em 2000

 

MODELO CRS

MODELO VRS

J

DMU

eficiência

Dentistas

Consultórios

Consultas

eficiência

Dentistas

Consultórios

Consultas

 

1

HCM

57,6% 

14

17

17,127

64,1% 

14

17

17,127

 

 

 

14

5,6

29,750

 

14

7

26,718

 

 

 

0,0%

- 67,1%

73,7%

 

0,0%

- 58,8%

56,0%

2

HNBE

55,0% 

18

12

21,025

65,4%

18

12

21,025

 

 

 

18

7,2

38,244

 

18

9,9

32,168

 

 

 

0,0%

- 40,0%

81,9%

 

0,0%

- 17,5%

53,0%

3

HNBR

39,6%

24

8

16,819

58,7%  

24

8

16,819

 

 

 

20

8

42,502

 

15,4

8

28,660

 

 

 

- 16,7%

0,0%

152,7%

 

- 35,8%

0,0%

70,4%

4

HNLA

67,4% 

10

5

14,332

67,4%

10

5

14,332

 

 

 

10

4

21,254

 

10

4

21,254

 

 

 

0,0%

- 20,0%

48,3%

 

0,0%

20,0%

48,3%

5

HNNA

66,8%

13

8

18,448

72,5% 

13

8

18,448

 

 

 

13

5,2

27,635

 

13

6,2

25,440

 

 

 

0,0%

- 35,0%

49,8%

 

0,0%

- 22,5%

37,9%

6

HNSA

62,2%

20

11

26,420

77,2%

20

11

26,420

 

 

 

20

8

42,510

 

19,5

11

34,214

 

 

 

0,0%

- 27,3%

60,9%

 

-2,5%

 0,0%

29,5%

7

HNRE

100%

10

4

21,250

100% 

10

4

21,250

 

 

 

10

4

21,250

 

10

4

21,250

 

 

 

0,0%

0,0%

0,0%

 

0,0%

0,0%

0,0%

8

PNNSG

61,8% 

38

27

49,907

83,9%

38

27

49,907

 

 

 

38

15,2

80,749

 

38

24,7

59,489

 

 

 

0,0%

- 43,7%

61,8%

 

0,0%

- 8,5%

19,2%

9

OCM

68,1%

94

66

135,964

100%

94

66

135,964

 

 

 

94

37,6

199,731

 

94

66

135,964

 

 

 

0,0%

- 43,0%

46,9%

 

0,0%

0,0%

0,0%

 

 

 

Na análise da eficiência parcial no modelo VRS em relação a cada input, apresentada nas figuras 2.1 e 2.2, verificou-se que as DMUs HNRE-00 e OCM-00 pertenciam à fronteira de eficiência em ambos os gráficos. Assim, a análise do modelo VRS nos conduz à conclusão de que HNRE deve ser considerada um benchmark para as demais unidades do mesmo porte, enquanto OCM deve ser considerada um benchmark dentre as unidades hospitalares de grande porte.

O estudo dos resultados obtidos até aqui revela, também, que a produtividade calculada em termos de consultas realizadas relativamente ao número de dentistas efetivo da unidade ainda é uma medida sujeita a distorções. Verificamos que o número de consultórios disponíveis modifica substancialmente os resultados da comparação que fosse feita exclusivamente em termos de produtividade dos recursos humanos. Realmente, verifica-se, na Tabela 2.6, que é na eliminação das folgas na utilização dos consultórios disponíveis que a eficiência da maior parte das DMU´s poderia ser aumentada. Logo, uma estratégia para elevar a eficiência envolveria, possivelmente, a elevação do número médio de dentistas nas unidades, ao contrário do que a análise em termos de produtividade simples indicaria.

 

 

 

3. MÉTODO DE MALMQUIST-DEA

 

O método de Malmquist-DEA resume-se em aplicar o algoritmo de programação linear de DEA para construção da fronteira de produção de um determinado período e depois para o cálculo da razão entre as distâncias de dois pontos de produção de períodos distintos de uma mesma unidade à fronteira assim construída. Determinamos, por exemplo, a distância do ponto de produção do período t à fronteira do período t, a distância do ponto de produção do período t+1 à fronteira do período t e calculamos a razão entre as distâncias.

Färe et alii (1994) calculam o índice de Malmquist-DEA (Mo) através da média geométrica de dois índices, onde o primeiro utiliza como referência a fronteira do período t e o segundo a fronteira do período t+1. A principal vantagem da utilização dessa média geométrica é evitar a difícil escolha entre qual das duas fronteiras de produção deve ser utilizada como referência para o cálculo do índice. Um valor de Mo maior que 1 indica um crescimento ou evolução do fator de produtividade total entre os períodos t e t+1, enquanto que um valor menor que 1 indica um declínio.

A Equação 3.1 representa a decomposição de Färe et alii (1994) para o índice de Malmquist. Nela e denotam, respectivamente, os volumes de inputs e outputs da DMU no instante t e  denota distância à fronteira do instante t medida em termos de eficiência relativa, conforme calculado pela DEA orientada para a maximização do output.

 

 

Equação 3.1. – Índice de Malmquist – média geométrica

 

 

 

Os seguintes problemas de programação linear devem ser resolvidos para o cálculo de na equação 3.1:

 

           

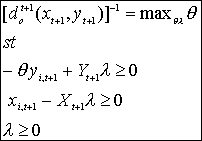
(A1)                                               (A2)

 

           

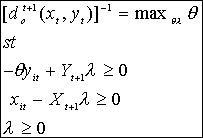
(A3)                                               (A4)

 

Nos problemas A3 e A4, onde os pontos de produção são comparados a tecnologias de períodos diferentes, o parâmetro  não precisa ser maior ou igual a 1, como se espera quando se calcula a eficiência no período corrente. O ponto pode ficar fora do conjunto de produção factível. Este fato ocorrerá com alta probabilidade se houver evolução tecnológica, no problema A3, onde um ponto de produção de um período t+1 é comparado com a tecnologia no período t. Obviamente, caso ocorra uma regressão técnica,  menor que um também será possível solução de A4.

Färe et alii (1994) apresentaram uma maneira equivalente de definir Mo, que permite uma interpretação do crescimento da produtividade em termos de fontes desta evolução:

 

Equação 3.2 – Índice de Malmquist – Forma Decomposta

 

Nesta decomposição, a razão fora dos parênteses mede a mudança na eficiência relativa e é chamada por Färe et alii (1994) de “mudança técnica”. Esta razão verifica se a produção da unidade está se aproximando ou se afastando da fronteira. Enquanto isso, a média geométrica das duas razões dentro dos parênteses mede a mudança da tecnologia entre os dois períodos avaliados em xt e xt+1 e é chamada por Färe et alii de “mudança na eficiência”. Estes índices parciais são importantes porque permitem verificar se um eventual aumento da eficiência relativa de um ano para o outro deve ser atribuído ao aumento da produtividade da unidade avaliada ou à contração da fronteira de produção.

Färe et alii (1994) discutem o uso da abordagem VRS no cálculo do índice de Malmquist. Calculando a “mudança na eficiência” em relação à fronteira VRS, obtêm o que chamam de “mudança na eficiência pura” e medem a mudança na escala de produção através da razão entre a “mudança na eficiência” e a “mudança na eficiência pura”. Esta caracterização é contestada, por exemplo, por Ray e Desli (1997). Estes calculam sua mudança na escala de produção através da média geométrica entre dois quocientes, o primeiro entre as razões das eficiências em relação às fronteiras CRS e VRS do instante t de DMUs com os valores da unidade em tela nos instantes t e t+1 e o segundo entre as razões das eficiências em relação às fronteiras CRS e VRS do instante t+1 das mesmas DMUs. Além disso, Ray e Desli (1997) defendem que a mudança técnica seja calculada com referência à fronteira VRS. Retornaremos ao confronto entre as abordagens CRS e VRS na Seção 6, ao introduzirmos a metodologia de Bjurek (1996).

 

 

4. RESULTADOS DA ANÁLISE DINÂMICA

 

Calculamos, inicialmente, o crescimento da produção e seus componentes no período de 1996 a 2000 utilizando Malmquist-DEA, segundo a proposta de Färe et alii (1994). A Tabela 4.1 apresenta os valores médios do índice de Malmquist e da decomposição de Färe et alii (1994). Estes valores constituem um sumário do crescimento da produtividade de todas as nove unidades durante todo o período analisado, de 1996 a 2000. Os valores em que se baseiam foram obtidos utilizando o DEAP (Coelli, 1996 e Coelli e Prasada-Rao, 2001).

 

Tabela 4.1. Média dos Índices de 1996-2000

DMU      

Índice de Malmquist

Mudança Técnica

Mudança na Eficiência

Mudança na Eficiência Pura

Mudança na  Escala

HCM

0,87

0,995

0,87

0,895

0,97

HNBE

1,06

1,12

0,94

0,97

0,97

HNBR

0,97

1,238

0,79

0,875

0,916

HNLA

1,09

1,19

0,92

0,91

1,01

HNNA

0,98

1,08

0,90

0,92

0,989

HNSA

1,01

1,11

0,90

0,95

0,95

HNRE

1,41

1,17

1,20

1,18

1,021

PNNSG

0,92

1,03

0,89

0,96

0,93

Com

1,04

1,08

0,965

1

0,965

Média

1,03

1,11

0,93

0,96

0,97

 

 

Podemos observar na Tabela 4.1 que houve crescimento médio de 2,9% por ano na produtividade ao verificarmos a média dos valores obtidos do índice de Malmquist. Ao observarmos os resultados de cada DMU, verificaremos que HNRE obteve o maior crescimento da produtividade total na amostra, com 40,6% em média, e que a mudança de eficiência contribuiu bastante para esse resultado.

A avaliação em termos de mudança técnica reduz a evolução das unidades que movimentam a fronteira no tempo. Para prover evidências para identificação das unidades inovadoras podemos observar as funções de distância e observar se:

TCk > 1

Dt(xk,t+1,yk,t+1) > 1

Dt+1(xk,t+1,yk,t+1) = 1,

onde k indica a unidade observada e TC denota mudança técnica. DMU’s satisfazendo estas condições contribuem para uma mudança da fronteira entre os períodos t e t+1. Aplicando este critério, podemos construir a tabela seguinte.

 

Tabela 4.2. Unidades que mais contribuíram para a mudança da fronteira

Período

Unidade

1996/1997

-

1997/1998

HNLA

1998/1999

-

1999/2000

HNRE

 

 

Os gráficos 1 e 2, abaixo, ilustram a decomposição do crescimento da produtividade, apresentando a evolução, ao longo do período, dos índices referentes às unidades HNLA e HNRE, respectivamente.

 

 

5. O MÉTODO DE BJUREK

 

Bjurek (1996) idealizou um índice de TFP definido como o quociente de um índice orientado para o output por um índice orientado para o input. Ao invés de definir o índice de produtividade baseado numa orientação de input ou output, esta formulação mede a mudança da quantidade de output na orientação para o output e da quantidade de input na orientação para o input. Enquanto, no índice orientado para o output, os recursos ficam fixos e o índice é o quociente tendo no numerador produção do ano t+1 e no denominador produção do ano t, no índice orientado para o input os produtos ficam fixos e o quociente tem no denominador recursos do ano t+1 e no numerador recursos do ano t.

 

Equação 5.1 – Método BJUREK

 

Para tornar o índice independente da escolha da fronteira inicial ou final, podemos usar também a média geométrica.

 

Equação 5.2. Método BJUREK – Média Geométrica

 

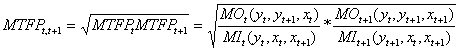
Esta formulação só é adequada ao cálculo relativo a fronteiras VRS. No ambiente CRS as medidas de eficiência nas orientações output e input dos dados de entrada e de saída idênticos se anulam tornando o índice mais simples:

 

Equação 5.3. Método BJUREK –abordagem CRS

 

 

É ilustrativa a comparação dos resultados obtidos através do cálculo do índice de Malmquist utilizando a metodologia de Bjurek(1996), relativamente ás fronteiras VRS e calculando a média geométrica, com os obtidos através da metodologia de Färe et alii (1994) para os anos de 1999 e 2000.

 

Tabela 5.1. Comparação da Metodologia de Bjurek com a Tradicional

DMU

MTFP

Malmquist

HCM

1

0,87

HNBE

1

1,15

HNBR

1

1,22

HNLA

0,97

0,93

HNNA

1

1,17

HNSA

1

1,16

HNRE

1,08

1,45

PNNSG

1

1,04

OCM

1,02

1,14

Média

1,01

1,11

 

Na tabela 5.1, percebe-se uma significativa diferença entre os índices calculados. Na abordagem de Färe et alii (1994), o índice de Malmquist englobando todos os componentes de variabilidade é obtido comparando com a fronteira CRS. Assim se há retornos decrescentes de escala, unidades pequenas podem gerar fronteiras de eficiência que as unidades maiores não podem atingir. A comparação com o resultado obtido através do emprego da metodologia de Bjurek (1996) permite avaliar esta conjectura. No caso, verifica-se que ela faz sentido e há maior homogeneidade na evolução das unidades examinadas, do ponto de vista das variáveis que pudemos levantar, do que sugerido pelos índices calculados pelo método anterior.

 

 

6. COMENTÁRIOS FINAIS

 

Este trabalho desenvolveu-se no sentido de aplicar a metodologia de análise de eficiência relativa e de fornecer maiores subsídios para análise do setor odontológico do Sistema de Saúde da Marinha através da quantificação das medidas da performance e da evolução da produtividade total calculados por DEA. Ficou evidenciado o poder dos novos enfoques aplicados de facilitar a avaliação das decisões de planejamento e de contribuir para orientar a revisão das técnicas de coletas de dados e operacionalização das variáveis. Por outro lado, a inclusão de outras variáveis, ainda não disponíveis, tornaria o modelo mais realista. Dentre estas variáveis destacamos, do lado dos recursos, o número de horas efetivamente dedicadas pelos cirurgiões dentistas à atividade-fim e o volume das despesas com material e, do lado dos produtos, o número de procedimentos cirúrgicos realizados.

 

 

7. REFERÊNCIAS BIBLIOGRÁFICAS

 

BANKER, R. D., CHARNES, A. e COOPER, W. W. (1984). “Some models for estimating technical and scale inefficiencies in Data Envelopment Analysis”, Management Science, 30 pp. 1078-1092.

 

BJUREK, H. (1996). “The Malmquist Total Factor Productivity Index”, Scandinavian Journal of Economics, 98, pp. 303-313.

 

CHARNES, A., COOPER W.W. e RHODES E. (1978). “Measuring the Efficiency of Decision Making Units”, European Journal of Operations Research, 2, pp.  429-444.

 

COELLI, T. e PRASADA-RAO, D. S. “Implicit Value Shares in Malmquist TFP Index Numbers”, CEPA Working Papers, Nº 4/2001, University of New England, 2001.

 

COELLI, T., “A Guide to DEAP - Version 2.1: A Data Envelopment Analysis (Computer) Program”, CEPA Working Papers, University of New England, 1996.

 

FÄRE, R. et alii, “The Measurement of Efficiency and Production”, Kluwer-Nijhoff, Publishing, Boston, 1985.

 

FÄRE, R. et alii (1994). “Productivity growth, technical progress, and efficiency change in industrialized countries”, American Economic Review,  84, pp. 66-83.

 

RAY, S. C. e DESLI, E. (1997). “Productivity growth, technical progress and efficiency change in industrialized countries” - Comment, American Economic Review, 87,  pp. 1033-1039.