ALGORITMOS DE CHAVE PÚBLICA:

ESTADO DA ARTE

ALMIR PAZ DE LIMA

UFF

Prazer e honra:

Claude Shannon: 1916 – 2001 – Communication Theory of Secrecy Systems – BSTJ 28 (1949), 656-715. Notices – AMS – Fev 2002.

RESUMO

Esta exposição abrange os seguintes tópicos:

Sistemas simétricos e assimétricos;

História refeita;

Problema cultural;

Propostas concretas;

Ilustração: El-Gamal;

Vale a pena conhecer fatoração polinomial?

DSA: canal subliminar;

“Hardware” para chave pública;

chave pública para cifra em cadeia.

Palavras-chave: Criptologia – Informação – Fatoração Polinomial – Algoritmos de Chave Pública.

1. Introdução

2. Sistemas Simétricos e Assimétricos

Os sistemas criptográficos clássicos usavam essencialmente a mesma chave secreta para cifrar e decifrar mensagens. São chamados simétricos, em oposição aos de chave pública, assimétricos porque possuem uma chave distribuída publicamente, isto é, sem segredo, mas o decifrador precisa dispor de uma informação adicional à chave pública.

Problema: distribuição de chaves. Solução: mudança de paradigma – chave e algoritmo de cifrar em claro.

As referências comentadas a seguir estruturam a história do desenvolvimento da área.

3. História Refeita

3.1.J. Ellis

The Possibility of Secure Non-Secret Digital Encryption. Communications – Electronics Security Group (CESG) – Report – Jan 1970.

Contribuição: Chave de decifrar = chave de cifrar criptografada.

3.2. W. Diffie, M. Hellman

New Directions In Cryptography

IEEE Trans IT, Nov 1976, Vol. 22, pp 644-654.

Contribuição: Construção de chave comum. Usada até hoje: D.H.

Não souberam propor solução concreta.

4. Problema cultural

Função de mão única: não achada até hoje.

Exemplos:

4.1. C = K x M – Inteiros

Divisão?

4.2. C = K x M – Matrizes

Obtenção da inversa?

4.3. C = K . M – produto escalar

Volta? Mochila.

Curiosidade: Minha parte (ostensiva). Em 2/12/1977 propunha “investigar linhas de pesquisa ... Teoria de Automata em Criptografia e cifras descritas ... ( (2) e RSA ) ... ”

Nota: P. Guam

Cellular Automaton Public-Key

Cryptosystems

Complex Systems Vol. 1. pp 51-56, 1986

5. Concretizações

1. C. Coks

A Note On Non-Secret Encryption

CESG Report – Nov. 1973.

2. R. Rivest, A Shamir, L. Adleman

Tech Memo n º 82 – LCS – MIT – April 1977.

On Digital Signatures And Pubic-Key Cryptosystems

Censura?

3. M. Gardner

A New Kind Of Cipher That Would Take Millions Of Years To Break.

Scientific American, Aug 1977

Quebrada em abril de 1994.

Comentários:

Dificuldade de fatoração: N = P x Q

(1) Não permite assinatura

C = M^N Mod N

(C, P, Q)→ M

Teorema Chinês dos Restos

(2) RSA: palestras e curso. Xexéo, Madeira, Ungaretti

C = M^E Mod N, N = PQ

M = C^D Mod N

ED = K (P-1) (Q-1)

Mais informação para o inimigo.

Meu resultado: D = 5 Mod 36, por exemplo.

4. – V.S. Miller

Use Of Elliptic Curves In Cryptography

Crypto´85 Proceedings – Springer – 1985 – pp 417-426

5. – K. Koyama

Fast RSA-TYPE Schemes Based On Singular Cubic Curves

Y² + aXY = X³ (Mod N)

Advances In Cryptology – Eurocrypt´95

Springer – pp 329-340

Comentários sobre 4) e 5) – Dificuldade de resolver o problema do logaritmo discreto em grupos construídos em curvas elípticas sobre corpos finitos.

Palestra Disnei, dono de experiência considerável no assunto.

6. – M. Williamson

Non-Secret Encryption Using A Finite Field

CESG Report – 1974

7. – T. ElGamal

A Public-Key Cryptosystem And A Signature Scheme Based On Discrete Logarithms

IEEE Trans IT, July 1985, pp 469-472

Comentários:

(6) – Sistema D.H. de geração de chaves.

(7) – Tem aleatorização.

Tamanho do criptograma (assinatura) é dobro do da mensagem.

Ilustração

Logaritmos discretos Mod P

2¹¹ Mod 577 = 317

P – Primo P = 2Q + 1, Q Primo

a : 1 < a < P-1 primitivo

x : 1 < x < P-1 secreto

aleatório

P >< 10 ²⁰⁰

Y = a^x Mod P

Chave pública: (P, a, Y)

Chave secreta: x

Mensagem – M, 1 < M < P-1

Aleatorizador: K , 2 < K < P-2

Criptograma (M, K) = (Y1, Y2)

Y1 = a^k Mod P

Y2 = (M * Y^k) Mod P

Decifração

M = (Y2 * (Y1^x)^-1) Mod P

Exemplo

P = 2579 = 2 x 1289 + 1

a = 2 ; x = 765

Y = 2⁷⁶⁵ Mod 2579 = 949

Mensagem: 1299

Aleatorizador: 853

Criptograma: (Y1, Y2)

Y1 = 2⁸⁵³ Mod 2579 = 435

Y2 = 1299 * (949⁸⁵³) Mod 2579 = 2396

Decifração

M = (2396 * (435⁷⁶⁵) ^-1) Mod 2579 = 1299

OBS: Há algoritmos eficientes para cálculo de potências módulo N.

6. Estado da Arte – 2002

São considerados seguros e eficientes os seguintes algoritmos: RSA, DSA, ElGAMAL, DH e análogos em curvas elípticas.

Notem as ressalvas a seguir, minhas e de outros.

- A. Menezes

Elliptic Curve Cryptosystems – Ready for Prime Time

Dr Dobb´s Web Site – Jan. 7, 1998

7. Contribuições

1 – Chave pública não é mais segura, que sistemas assimétricos: falsa confiança.

A) Não há prova de que problemas sejam intratáveis.

B) Argumento de tempo:

- Wiles (Princeton) – 1995

Último teorema de Fermat

350 anos – curvas elípticas

- Professor Assistente U. Illinois

100 anos

Problema das quatro cores

1973

C) Argumento de complexidade:

Mochila – NP – Completo

1978-1982

Tese Aldner – UFRJ – abril 1988

McEliece – 1978

Decodificação de códigos lineares

NP completo

Usa código Goppa (decodificador simples)

como chave secreta.

A matriz do código, disfarçada, é a chave pública

Tem aleatorização.

Cláudia Arbex – Tese Mestrado

IME – 1982

Sistema Simétrico – Crypto´86

Quebrado por criptologistas russos – notícia de uso pelo Exército Americano.

- V.I. Korzhik, A. I. Turkin

Cryptanalysis Of McEliece Public Key Cryptosystem – pp 68-70. Eurocrypt´86

D) Argumento de diversidade

RSA generalizado para polinômios:

B. L. V. Freire

Proposta de um sistema de chave pública

Tese de Mestrado – IME – 1981

D. W. Kravitz

The Application Of Finite Polynomial Rings To Number Theoretic Cryptosystems.

Tese PHD – U. Southern California – May 1982

Kravitz – NSA

Patente DSA – 1993

Quebrados (?)

Tese interrompida UFF comparando em detalhes os dois trabalhos e tentando contornar a quebra.

E) Flannery

Cryptography: An Investigation Of A New Algorithm vs RSA.

http://www.cayley-purser.ie/

Usa matrizes 2 x 2 sobre ZN, N = PQ.

Chave pública: N, A, B, G

A, B, G matrizes

Chave secreta: matriz C

Tem aleatorização: G^s.

Prova que obtenção de C é difícil.

Quebrado: é possível construir múltiplo escalar tC da matriz secreta, para algum t. Daí, com valores públicos, recupera-se a mensagem, sem identificar C.

T. Okamoto

Fast Public Key Cryptosystem Using Congruent Polynomial Equation. Electronic Letters Vol 22 n º 11, 1986, pp 581-582

N = P² Q

Quebra parcial: valores baixos e altos de um parâmetro público

Quebra total, sem fatoração: frações contínuas.

F.X. Li

How To Break Okamoto´s Cryptosystem By Continued Fraction Algorithm. Asiacrypt´91 – Abstracts – 1991 pp 285-9

Minha solução independente, 3 anos depois. Igual. curso UFF.

D. Boneh

Twenty Years Of Attacks On The RSA Cryptosystem

Notices – AMS – Feb. 1999

pp 203-213

Não usar módulo comum

D > 1/3 (N ^1/4) ou E > N ^1,5

(posso contornar E > N ^1,5)

- Conjectura: D > N ^1/2 se E < N?

Não usar E pequeno

Recomendado: E >= 65.537

Mensagem aleatorizada com muitos bites

Ataques de tempo e potência

Tratamento matemático rigoroso

CAPES: Matemática marginal!

8. Fatoração polinomial?

H. Riesel – Inst. Real Tecnologia - Estocolmo – Suécia

Prime Numbers And Computer

Methods For Factorization

Birkhauser – 1994

“... há muito espaço para aperfeiçoamento dos algoritmos de fatoração existentes. É possível chegar a algoritmo aproximadamente linear (em Log N)... ” pag 223

“... não há maneira de estimar a probabilidade de acontecer (ou de já ter acontecido...) a descoberta de um método de fatoração ... polinomial ... . Neste sentido, a criptografia RSA é, e será sempre, insegura”. pag 236-7

Autor russo (?)

Quebra RSA 512 bites (154 decimais) na Holanda. Implementações comerciais.

B. Schneier

Applied Cryptography - Wiley – 1994

“... excetuando RSA, ElGAMAL, DSA, DH, antes de usar qualquer outro algoritmo ... faça uma pesquisa na literatura para ver se não foi quebrado ...” pag 130

Comentário: quebra sem divulgação

ELLIS Enigma – ULTRA – 2 ª Guerra McEliece – Russos - URSS

9. Sistema DSA

Agosto 1991 – NIST – FIPS

Proposta

Pode ser usado para cifrar RSA e ELGAMAL (Schneier – pp 310-1)

Tem canal subliminar

G. Simmons:

“... pode passar bites de chave melhor que ElGAMAL...”

Subliminal Communication Is Easy Using DSA

Advances In Cryptology – Eurocrypt´93

Springer – 1994 – pp 218-232

Schneier: “Não use se você não confia no implementador”.

Cripto AG – Irã.

M.S. Conn – NSA

Carta para o jornal Houston Chronicle, 10 Jun. 1992

“... DSA tem endosso da NSA para assinar dados ostensivos processados em certos sistemas de inteligência e, mesmo, dados sigilosos em sistemas selecionados”.

Comentário: não é irrestrito. Assinatura não é exclusiva de chave pública, a IBM tem, pelo menos, duas patentes de assinatura com o DES.

Será que a NSA não tem solução semelhante?

10. Solução em “hardware” para chave pública

Y. Desmedt, J.J. Quisquater

Public-Key Systems Based On The Difficulty Of Tampering (is there a difference between DES and RSA?)

Advances In Cryptology – Crypto´86

Springer 1987 – pp 111-117

Proposta de Ellis, provavelmente desconhecida pelos autores

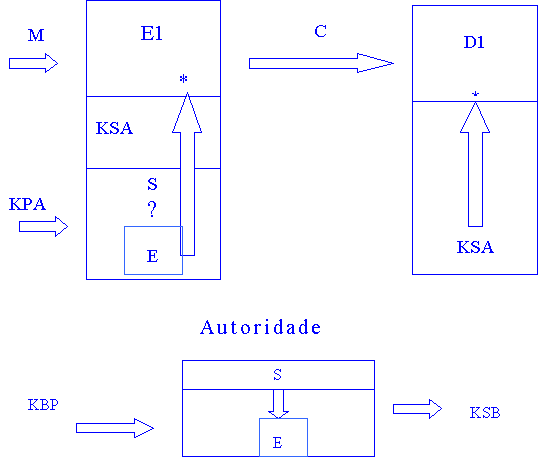
Hipótese – Pastilha resistente à intrusão (“Tamper-Free”)

Vantagem: velocidade E1, D1: simétricos

11. Nome como chave pública

W.M. Raike

The RPK Public Key Cryptographic System – Technical Summary -http://crypto.swdev.co.nz - 1993-1996

Baseado em gerador de aleatórios com misturador (GEFFE)

Chave pública: vetor de estados dos geradores

Chave secreta: deslocamentos dos estados iniciais

Cifração: cadeia de bites

D.D. Buckley, M. Beale

Public Key Encryption Of Stream Ciphers - Eurocrypt´86

Abstracts Of Papers (não publicados os anais!)

Aleatorização

Problema do logaritmo discreto em corpos finitos (CG (2 ^P))

Permite assinatura, embora operações de cifração e decifração não comutem.

Chave “grande”

Disnei – agradecimento

Não conheço quebra

12. Conclusão

A criptografia de chave pública não é uma panacéia. Nenhum sistema criptográfico além da “chave-de-uma-só-vez” é incondicionalmente seguro, e é preciso que não nos iludamos com argumentos falaciosos que “comprovam matematicamente” a segurança dos sistemas assimétricos.

Talvez seja o caso de fazermos com sistemas assimétricos o que se tem feito com sistemas simétricos, seguindo a sugestão de Shannon – combinar vários passos de substituição e de transposição.

Outra possibilidade: tentarmos concretizar o modelo de Ellis: chave pública = criptograma da chave secreta.