RESTRINGINDO FLEXIBILIDADE DE PESOS EM DEA

UTILIZANDO ANÁLISE DE REGRESSÃO MSEA

Antonio Allen Meireles Alcântara

Programa de Engenharia de Produção - COPPE/UFRJ

allen@br-petrobras.com.br

Annibal Parracho Sant’Anna

Departamento de Engenharia de Produção - UFF

annibal@plugue.com.br

Marcos Estellita Lins

Programa de Engenharia de Produção - COPPE/UFRJ

estellit@iis.com.br

Abstract

In this paper we present a procedure based on the use of Minimum Sum of Absolute Errors (MSAE) regression for the treatment of factor weights in DEA, in the case where the decision assessed involves a single output. It develops and presentsAn alternative method to limit the range within wichwhich these factor weights are allowed to vary is developed. The objective here is to work provide an automaticone way to derivein which numerical boundsconstraints can be placed for the case where the decision assessed involves a single output.

Palavras-chave: DEA, restrições de peso, medição de eficiência, regressão linear múltipla MSAE.

1. Introdução

Neste artigo apresentamos um método para restringir a flexibilidade de pesos dos fatores na utilização de Data Envelopment Analysis (DEA), metodologia desenvolvida para avaliar eficiência relativa de unidades produtivas através de análises realizadas nos níveis de utilização de suas entradas, ou inputs,eus inputs objetivando a produção de seus outputsuas saídas, ou outputs. . . No modelo dos multiplicadores, CCR, Mais especificamente, as eficiências são resultantes de maximização da razão da soma de saídasoutputs ponderadaos pela soma de entradas inputs ponderadaos da unidade sob avaliação. Na forma originalmente apresentada por Charnes, Cooper e Rhodes (1978)[1], DEA permite total flexibilidade de pesos utilizados nas ponderações, de tal forma que cada unidade alcança sua eficiência máxima não levando em conta qualquer prioridade ou limitação na utilização dos fatores.

Esta flexibilidade permite, por um lado, que cada unidade busque sua eficiência segundo mixcomposição, ou mix, de pesos de inpuentradas ts e saídasoutputs própriaos, sem necessidade de submeter-se a uma única composiçãoo mix para todas as unidades. Por outro lado, esta flexibilidade leva a situações inaceitáveis, devido a duas características dos modelos DEA [15]):

1. As regiões Pareto-ineficientes, nas quais as DMUs apresentam pesos nulos atribuídos a algumas entradas ou saídas.ns inputs ou outputs.

2. Os vértices do conjunto de possibilidades de produção, pontos em que se verifica uma infinidade de mixcomposições de pesos ótimos (soluções ótimas alternativas do modelo DEA dos multiplicadores).

Freqüentemente em aplicações práticas de DEA, onde não são impostas restrições aos pesos, encontramos soluções impróprias, pois a eficiência de algumas unidades é alcançada quase que exclusivamente devido a um determinado fator. Ocorre, ainda, muitas vezes, as distribuições dos pesos apresentarem-se completamente diferentes para as diferentes unidades.

. A maior parte deles incorpora valores de julgamentos a priori realizados por especialistas, que freqüentemente causam controvérsias. Resumidamente, podemos dizer que os critérios e procedimentos desenvolvidos até aqui passam pelo estabelecimento de restrições arbitrárias diretas nos pesos [2], restrições também arbitrárias sobre a proporção da importância de determinado output de uma DMU j em relação aos demais outputs [3], e estabelecimento de princípios de ´´regiões de segurança´´ , onde restrições são introduzidas para incorporar na análise uma ordenação relativa dos diversos inputs ou outputs [4], [5].

O artigo é organizado da seguinte maneira: na Seção 2 são destacados os principais trabalhos sobre restriçãocao de pesos em DEA, na Seçãocao 3 introduzimos a técnica de estimação MSEA apresentando os procedimentos para a obtenção dos estimadores pontuais e por intervalo; na Seção 4 avaliamos a utilização de MSEA aos dados da aplicação, calculamos seus estimadores e a seguir ponderamos os estimadores pelaos inputsentradas, terminando com a aplicação da metodologia DEA com e sem restrições aos dados, verificando suas diferenças; finalmente concluímos o artigo na Seção 5 com comentários finais.

2. Estudos Anteriores

Diversos trabalhos para impor limites a pesos de fatores têm sido desenvolvidos e publicados , destacando-se:

· Restrições Diretas nos pesos

Desenvolvido por Dyson e Thanassoulis (1988) e generalizado por Roll, Cook e Golany (1991). Segundo este método, impõem-se limites numéricos diretamente aos multiplicadores, da forma:

Q2_i £ V_i £ Q1_i para as entradas,os inputs

P2_r £ U_r £ P1_r para as saídas,os outputs

B₀ = S V_i X_i0.

· A Região de Segurança (Assurance Region-AR)

Desenvolvido por Thompson, Langemeier, Lee, Lee e Thrall (1990).. As restrições AR são do tipo:

U_r £ a_rs U_s, " r ¹ s

V_i £ b_ij V_j " i ¹ j

onde a_rs e b_ij são definidos pelo usuário.

Esta é a chamada Região de Segurança de tipo I (Assurance Region I – AR I).

A Região de Segurança de tipo II (Assurance Region II – AR II), apresentada por Thompson et al. (1990), relaciona os pesos das entradas e saídas.os inputs e dos outputs.

· Método Cone Ratio

Desenvolvido por Charnes, Cooper, Wei e Huang (1989). Este método permite uma transformação da base de dados original de modo a que o modelo com restrições possa ser implementado em um software para modselos DEA básicos . Uma vez obtidos os resultados, os dados devem ser. transformados para a forma original para que se possaa fim de interpretá-los.

· Restrição às entradas e saídasaos inputs e outputs virtuais

Do ponto de vista do usuário, é, as vezes difícil estabelecer limites aos multiplicadores, levando em conta as unidades de medidas dos iinputs e outputsas entradas e saídas. Uma alternativa mais amigável é estabelecer limites f_r e y_r à saídaao output virtuail r de uma DMU j, o que foi proposto por Wong e Beasley (1990).. A restrição à saída ao output virtual r é da forma

,

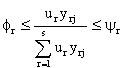
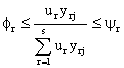
onde

representa a saídao output v virtual total da DMU j. Este tipo de restrição, no entanto, acarreta problemas de inviabilidade de difícil solução.

· Restrição contingente das entradas e saídasos input e outputs virtuais

Propõe a imposição de limites relativos às participações de cada input (ou output)entrada ou saída na entradao input v virtual. Foi, e foi proposta por (Pedraja-Chaparro et al, 1997). Produz restrições da seguinte forma:

c_iV₁X_1j £ V_iX_ij £ d_i V₁ X_1j,

para i > 1, onde c_i e d_i são determinados pelo usuário.

Este tipo de restrição aos pesos é “contingente” porque o padrão dos pesos selecionados depende dos níveis das entradas e saídasos inputs e outputs utilizados pela DMU .

Os métodos apresentados para introduzir as restrições nos pesos podem ser classificados da seguinte forma, (Pedraja-Chaparro et al., (1997)).:

	Tipo de Restrição
Pesos (multiplicadores)	Absoluta	Relativa
Original	Dyson & Thanassoulis (1988) 1988) Roll, Cook & Golany (1991)	Thompson, Langemeier, Lee, Lee & Thrall (1990)
	Método Cone Ratio (1989)
Virtual	Wong & Beasley (1990)	Pedraja-Chaparro et al. (1997)

O critério adotado neste trabalho utiliza o ajustamento preliminar de um modelo de regressão linear y= Sx_i b_i + e, onde o parâmetro b_i indica a mudança esperada na variável dependente y por unidade adicionada à variável x_i, quando as outras coordenadas do vetor x de variáveis explicativas permanecem inalteradas. No nosso caso, seguindo esse conceito, os parâmetros b_i representam as importâncias relativas de cada input na entrada na determinação da saídao output y. Depois de estimados estes parâmetros, calculamos intervalos de confiança para as estimativas dos b´s. Os limites b_min e b_max destes intervalos, serão utilizados na construção de proporções que delimitarão os pesos das entradasos inputs na determinação das eficiências utilizando DEA.

Dentro das diversas alternativas de estimação de parâmetros em regressão linear, como por exemplo a popular Mínima Soma dos Erros Quadráticos (MSEQ), a Mínima Soma dos Erros Relativos (MSEA) e também a Mínima Soma dos Erros Absolutos (MSEA), optamos pelo último método, pois se apresenta como a alternativa mais robusta. A busca de alternativas robustas se justifica por ser a presença de outliers uma provável causa dos pesos extremos que queremos evitar. Adotando o algoritmo de minimização da soma dos valores dos resíduos na regressão linear, estaremos sendo coerentes com uma idéia central de DEA, que é a de não descartar outliers, admitindo a existência de informações relevantes neste tipo de observação.

Ao contrário de grande parte das abordagens anteriores, a utilização de regressão estatística neste trabalho aparece como um complemento, e não como uma alternativa à metodologia DEA. Nosso objetivo é oferecer uma possibilidade de refinamento para propiciar que seus resultados se apresentem coerentes com a realidade das aplicações.

O artigo é organizado da seguinte maneira: na Seção 2 introduzimos a técnica de estimação MSEA apresentando os procedimentos para a obtenção dos estimadores pontuais e por intervalo; na Seção 3 avaliamos a utilização de MSEA aos dados da aplicação, calculamos seus estimadores e a seguir ponderamos os estimadores pelos inputs, terminando com a aplicação da metodologia DEA com e sem restrições aos dados, verificando suas diferenças; finalmente concluímos o artigo na Seção 4 com comentários finais.

3. 2. A Regressão MSEA

3.1 Introdução

O algoritmo da Mínima Soma dos Erros Quadráticos (MSEQ) há muito tempo ocupa posição privilegiada na estimação dos parâmetros de modelos de regressão linear devido, principalmente, à relativa simplicidade da teoria. Tem presença obrigatória em todas as rotinas de computadores para cálculo de estimadores. Entretanto, seus resultados têm de ser questionados quando a distribuição das perturbações não é Normal. A presença de outliers, muitas vezes, revela que o erro aleatório possui uma distribuição complicada pela mistura de alguma parcela discreta ou representante de uma família de distribuições com cauda mais acentuada, como, por exemplo, as de Cauchy e LaLaplace (ver Blaterg e Sargent (1971)). [6].

Um método para avaliarmos esta distribuição dos erros, apresentado em Montgomery e Peck (1992)[7], fornece um bom critério para verificarmos se estimadores de MSEQ devem ser utilizados em determinada aplicação. O método consiste em plotar em ordem crescente os erros, ou seja, e_[1] < e_[2] < ... < e_[n3] contra a probabilidade cumulativa P_i = [(i – ½)]/ n. O gráfico resultante, dependendo de sua forma, indicará presença ou não de outliers que, em caso positivo, sugere a utilização de outra alternativa para os estimadores.

O Método das Mínimas Somas dos Erros Absolutos (MSEA) supera as deficiências encontradas pelo MSEQ na existência de outliers. Este método é menos sensível à existência de dados extremos, podendo ser demonstrado que estimadores de mínima soma dos erros absolutos são de máxima verossimilhança quando os erros seguem uma distribuição de Laplace, conforme Blaterg e Sargent (1971). [6].

Durante muito tempo, a descoberta de algoritmos computacionais para solução do problema dee

min S ÷ y_i - x_ibú em modelos de regressão linear múltipla foi uma barreira à utilização do método. Uma contribuição de Charnes, Cooper e Ferguson (1955)[8] foi formular a regressão MSEA como um problema de programação linear. Nas últimas décadas vários algoritmos eficientes têm sido propostos, ver Barrodale e Roberts (1973) e Zhang (1993).[9],[10].

Ao trabalharmos regressão linear em conjunto com DEA, onde outliers são importantes nas análises, devemos escolher um método que supere este problema de alta sensibilidade aos dados extremos sem admitir a exclusão de dados. Esta é uma vantagem da regressão de Mínima Soma dos Erros Absolutos (MSEA) sobre outros métodos apresentados em Narula e Wellington (1985)[11], como alternativas robustas à regressão MSEQ.

3.2 Estimadores de MSEA

Considere o modelo de regressão linear múltiplo y = b₀ + b₁x₁ + ... + b_k + e (1), onde y é uma variável dependente; x ₁,..., x_k são k variáveis regressoras; b₀, b₁, ...b_k são k + 1 constantes desconhecidas e e representa o erro aleatório produzido pelo modelo possuindo função de densidade denotada por f(e).

O estimador obtido pelo método da Mínima Soma dos Erros Absolutos (MSEA) b de b minimiza

å_iⁿ = çy_i - x_ib ç (1)

para todos os valores de b, onde y_i é o i-ésimo elemento do vetor Y e x_i é a i-ésima linha da matriz X, sendo n o número de observações. O modelo em (1) pode ser escrito na forma matricial como Y = Xb + e. O procedimento para encontrarmos o estimador MSEA pode ser formulado através do seguinte PPL:

Minimizar 1'e⁺ + 1'e^-

Sujeito a Xb + e⁺ - e^- = Y

e⁺ , e^- ³ 0

b irrestrito em sinal, sinal,

onde o estimador MSEA b é um vetor k x 1, 1 é um vetor n x 1, sendo

e_j⁺ = (y_j – x_j b) se y_j – x_j b ³ 0

e_j^- = -(y_j – x_j b ) se y_j – x_j b < 0

4. Um exemplo na utilização de MSEA com DEA

4.1 Obtenção dos estimadores estimadores

Ilustraremos a utilização de estimadores MSEA através de um exemplo. Os dados, com duas variáveis regressoras e uma variável dependente para 25 observações vêem de Montgomery e Peck (1992) [7], com dados sobre tempo de entrega. Utilizando oprograma de computador para resolver o PPL da Seção 2.2, com o critério MSEA, encontramos o seguinte modelo com duas variáveis regressoras com o critério MSEA: Y = 3.66210 + 1.42721X₁ +0 .0143X₂ . (2).

Utilizando resultados de inferência estatística baseados em Narula (1987)[12], calcularemos intervalos de confiança para os estimadores de MSEA da regressão (2).

Para o estimador b_i, a um intervalo de confiança de (1-a) 100%, t teremos a seguinte amplitude

b_i - z_a/2 t (X’X)_ii^-1/2 £ b_i £ b_{i +} z_a/2 t (X’X)_ii^-1/2

onde (X’X)_ii^-1 é o i-ésimo elemento da diagonal de (X’X)^-1 e t um estimador proposto em Birkes e Dodge (1993) e Mckean e Schhrader (1987) dado por seguinte forma

[13],[14] da seguinte forma

t = n*^1/2 (e_{[n*- m + 1]} - e_[m])/4 , onde m = (n* + 1)/2 - n^*1/2 e ,

n* sendo o número de

resíduos diferentes de zero e e_[1], e_[2], ..., e_[n*] são os resíduos diferentes de zero ordenados em ordem crescente.

No exemplo em estudo, (X’X)₂₂ ^-1 = 0.0027, n* = 22, m = (22 + 1)/2 – 4.69 = 6.81,

t = 4.69 (e₂₀₁₆ – e₇)/4 = 4.69 (1.08681.1753 + 0,66594)/4 = 2.0552.1582 para a/2 = 0.005,

b₁ – (2.34074)(2.0552.1582) ( 0.0027)^1/2 £ b₁ £ b₁ + (2.34074)(2.0552.1582) ( 0.0027)^1/2 e

1.17731945 £ b₁ £ 1.67716596 (3)

Calculando agora o intervalo para b₂ : (X’X)₃₃^-1 = 0.00000123,

b₂ – (2.34074) (2.0552.1582) (0.00000123)^1/2 £ b₂ £ b₂ + (2.34074) (2.0552.1582) (0.00000123)^1/2 e

0.0089093 £ b₂ £ 0.019692 (4)

4.2 Ponderando os Estimadores pelas Escalas das Entradasos Inputs

É importante observar que, simplesmente analisando os estimadores pontuais obtidos na Seção anterior, não puodemos concluir muita coisa a respeito da importância de cada entradainput nna determinação da saídao output y. Logicamente, os valores dos estimadores b₁ e b₂ são influenciados pelas escalas de valores daos correspondentes inputs entradas x₁ e x₂.

Devemos propor um procedimento razoável para eliminarmos esta influência, de forma que tenhamos um parâmetro que indique as reais parcelas de contribuição na determinação da saídao output feita por cada entradainput. Uma maneira simples de obtermos este

parâmetro é relacionando os estimadores b_i´s com a média dos dados observados da variável x_i, conforme mostrado a seguir:

Y_i = [ b_i . S x_ij / n] / S [b_i . S x_ij / n].

No caso em estudo, teremos Y₁ = 0,681371 e Y₂ = 0,318729.

Estas medidas pontuais podem ser utilizadas para formar os intervalos Y_{i min} e Y_{i max} através das amplitudes relativas dos intervalos de confiança (3) e (4).

Para o intervalo de b₁ a amplitude do intervalo foi de (1.67716596 – 1.42721)/1.42721= 0.1751629 ou 17.516.29%. Da mesma forma, para b₂ teremos uma amplitude percentual de 37.0634.26%

Utilizando estes percentuais encontramos os intervalos possíveis para os pesos daos entradas inputs na determinação da saídao output:.

0.563259 £ Y₁ £ 0.800082

(5)

0.200019 £ Y₂ £ 0.436848

4.3 Utilizando Estimadores MSEA ponderados como Restrição aos Pesos em DEA

Utilizando os dados referidos, de Montgomery e Peck (1992), [7], geramos a Tabela A (ANEXO), com os escoresscores de eficiência, os respectivos conjuntos referência, ou (peer groups,) e ainda a contribuição de cada entradainput na obtenção da eficiência. O modelo utilizado foi o CCR com orientação para a minimização das entradasinputinput, sem restrição aos pesos dos fatores formalizado assim:

.

Seja a DMU_o a unidade a ser avaliada. Nós resolvemos o seguinte problema de programação fracional para obter os valores dos pesos das entradasos inputs v_i (i=1,2) e o peso dao únicao saída output u como variáveis.

Max f = (uy_o / v₁x_1o + v₂x_2o) (6)

Sujeito a (uy_j / v₁x_1j + v₂x_2j) £ 1 (j=1,2,...,25) (7)

Sendo v₁, v₂ ³ 0 e u ³ 0 (8)

Este é um programa de programação não linear que pode ser convertido em um PPL.

Podemos observar, na Tabela A, por exemplo, que todas as observações 4, 5, 10, e 12 alcançam suas eficiências baseadas exclusivamente no fator X_1, o que, na prática, possivelmente, não se apresenta como um resultado razoável.

Os pesos representam um valor relativo que proporciona o melhor escorescore possível para uma determinada unidade, além disso, esse sistema de pesos deve garantir que para todas as unidades, nenhuma alcance um um score escore de eficiência acima da unidade. Nestas condições, é comum algum fator de menor relevância adquirir um peso relativamente alto, gerando uma unidade eficiente basicamente às custas desse fator, tendo por outro lado atribuído peso nulo a fatores mais relevantes, sendo isso inaceitável do ponto de vista prático.

Utilizando agora o mesmo modelo CCR-I (Equações 6-8) acima, tendo a Equação (8) alterada para (8´) conforme resultados obtidos em (5), teremos

0.5632 £ v₁ £ 0.8100 e 0.1900 £ v₂ £ 0.4368 (8´)

representando as restrições aos fatores calculadas anteriormente. Assim, encontramos a Tabela B em anexo.

acrescido das restrições impostas aos inputs conforme restrições adicionais em (5), teremos a Tabela B (ANEXO).

Como podemos observar na Tabela B, as restrições ão aos pesos tornaram ornou o resultado da avaliação de desempenho mais balanceada, no sentido de que todasos asos entradasinputs participam de uma maneira mais aproximada ao ajuste realizado pela regressão linear realizada no início deste trabalho. Também observa-sese observa, comparando as duas Tabelas, uma maior discriminação entre as observações para o modelo com restrições.

5. Comentários Finais

O conjunto de dados que escolhemos não se caracteriza como especialmente adequado para o ajustamento pelo critério de minimização da soma dos valores absolutos dos resíduos. Os resíduos da regressão de mínimos quadrados apresentam um padrão típico de uma amostra proveniente de uma distribuição com cauda mais fina que uma Normal.

O ajuste obtido por Mínimos Quadrados é y = 2.3412 + 1.6159x₁ + 0.0143x₂ com R² = 0.9596 e os intervalos de confiança produzidos sob as hipóteses clássicas conduzem a restrições para os pesos e resultados finais para as medidas de eficiência muito próximos dos que obtivemos com os intervalos de confiança maiores produzidos pelo ajustamento por MSAE. Demonstramos desta forma a robustez do procedimento proposto para variações na especificação das perturbações. É um procedimento que leva em conta a possível presença de outliers, mas que se comporta satisfatoriamente, mesmo quando os dados, ao contrário, se apresentam muito concentrados.

É importante destacar que, mesmo com intervalos de confiança mais largos do que o possivelmente necessário, ainda obtivemos restrições efetivas, no sentido de conduzir a uma envoltória mais realista. Obtemos desta forma um procedimento geral para produção de restrições aos pesos. Este caráter geral, aliado à sua relativa simplicidade, permite que ele seja usado de forma automática, em lugar dos procedimentos ad hoc.

AFinalmente, acreditamos que a técnica de restrição de multiplicadores proposta neste artigo, aqui aplicada a somente uma saída output, pode ser generalizada a situações de váriaos saídasoutputs. Sugeriríamos, para este caso, na etapa inicial, umaUma recomendação para estudos posteriores seria análise de a utilização prévia de correlação canônica, conforme Arnold et ali (1996).

Referências

ALLEN R., ATHANASSOPOULOS A., DYSON R G e THANASSOULIS, E. (1997), “Weights Restrictions and Value Judgments in Data Envelopment Analysis: Evolution, Development and Future Directions”, Annals of Operations Research, vol. 73, pp. 13-34.

ARNOLD V, BARDHAN I, COOPER W, KUMBHAKAR S. (1996), New uses of DEA and statistical regressions for efficiency evaluation and estimation, Annals of Operations Research 66, pp 255-277.

BARRODALE I, ROBERTS F D. (1973), An improved algorithm for discrete L₁ linear approximation. S.I.AM., J. Numer. Anal. 10, 839-848

BIRKES D, DODGE Y. (1993) Alternative Methods of Regression. John Wiley and Sons, Inc., New York.

BLATERG R, SARGENT T. (1971) Regression With Non-Gaussian Stable Disturbances: Some Sampling Results, Econometrica, Vol. 39, No 3, 501-510

CHARNES A, COOPER W e FERGUSON R. (1955). Optimal estimation of executive compensation by linear programming. Management Science

CHARNES A, COOPER W e RHODES E. (1978) Measuring efficiency of Decision making, European Journal of Units Operational Research, 2(6): 429-444.

CHARNES A, COOPER W, WEI Q. L., HUANG Z. M. (1989) “Cone Ratio Data Envelopment Analysis and Multiple Objective Linear Programming”, International J. of Management Science, Vol. 20, pp.1099-1118.

CHARNES A, COOPER W, HUANG Z. M., SUN, D. B. (1990), “Polyhedral Cone-Ratio DEA Models with an illustrative application to Large Commercial Banks”, Journal of Econometrics, v. 46, pp. 73-91.

Dyson R G, Thanassoulis E. (1988), “Reducing Weight Flexibility in Data Envelopment Analysis”, Journal of the Operational Research Society, v. 39, n. 6, pp. 563-576.

KORNBLUTH, J. S. M. (1991), “Analysing Policy Effectiveness using Cone Restricted DEA”, Journal of the Operational Research Society, Vol. 42, Nº 12, pp. 1097-1104.

MCKEAN J, SCHHRADER R M. (1987), Least absolute errors analysis of variance, Statistical Data Analysis Based on the L₁ – Norm and Related Methods, Elsevier Science Publishers B, 297-305.

MONTGOMERY D C, PECK (1992) E A, Introduction to Linear Regression Analysis, Wiley & Sons.

NARULA S, WELLINGTON J. (1985), Interior Analysis for the Minimum Sum of Absolute Errors Regression, Technometrics, Vol. 27, No 2, 181-188.

NARULA S. (1987) The Minimum sum of absolute errors regression, Journal of Quality Technology, 19, 37-45

PEDRAJA-CHAPARRO R., SALINAS-JIMENES J., SMITH P. (1997), “On the Role of Weight Restrictions in DEA”, Journal of Productivity Analysis, Vol. 8, pp. 215-230.

ROLL Y., COOK W., GOLANY B. (1991), “Controlling Factor weights in DEA”, IIE Transactions, Vol. 23, pp. 2-9.

Thompson R G, LANGEMEIER L N, LEE C, LEE, E., THRALL R. (1990), “The Role of Multiplier Bounds in Efficiency Analysis with Application to Kansas Farming”. Journal of Econometrics, v. 46, pp. 93-108.

WONG Y H B, BEASLEY J E. (1990), “Restricting Weight Flexibility in DEA”, Journal of the Operational Research Society, vol. 41, pp. 829-835.

ZHANG Y. (1993) Primal-Dual interior point approach for computing l₁ solutions and l_µ solutions of overdetermined systems, Journal of Optimization Theory and Applications, 77, 323-341

ANEXO

Tabela A

Eficiência das unidades, , contribuição dasos inputs entradas e referênciase conjunto referência Sem Restrição de Multiplicadores – Modelo CCR-I
Observação	Eficiência %	Referência	Contribuição X1	Contribuição X2
19	100,00	-19	740,24596 (97,12%)	260,00728 (2,87%)
7	100,00	7-	890,44500 (99,77%)	110,00100 (0,22%)
4	100,00	4-	960,15703 (97,12%)	40,00464 (2,87%)
10	100,00	10-	1000,17442 (99,88%)	00,00021 (0,12%)
3	94,02	77 e 10	880,29307 (99,88%)	120,00035 (0,12%)
2	93,88	710	920,30612 (99,88%)	80,00037 (0,12%)
13	83,54	710	930,23207 (99,88%)	70,00028 (0,12%)
14	80,28	77	910,15244 (99,88%)	90,00121 (0,12%)
18	74,55	419	640,09168 (97,12%)	360,00271 (2,87%)
16	70,68	77 e 10	910,09140 (99,88%)	90,00011 (0,12%)
25	70,369,62	44 e 7	920,23057 (99,77%)	80,00052 (0,22%)
15	67,37	44	900,09993 (99,77%)	100,00022 (0,22%)
8	67,03	47	940,13383 (99,77%)	60,00030 (0,22%)
9	66,88	44 e 7	900,30050 (99,77%)	100,00006 (0,22%)
17	66,86	47	930,15505 (99,77%)	70,00035 (0,22%)
6	65,71	47	900,12917 (99,77%)	100,00029 (0,22%)
11	64,57	47	910,05699 (99,77%)	90,00013 (0,22%)
5	60,95	47	950,15780 (99,77%)	50,00035 (0,22%)
24	60,30	77 e 10	910,11403 (99,88%)	90,00013 (0,12%)
1	57,93	710	910,13023 (99,88%)	90,00016 (0,12%)
12	56,27	47	950,09539 (99,77%)	50,00021 (0,22%)
21	54,16	419	710,07070 (97,12%)	290,00209 (2,87%)
22	52,83	47	930,03594 (99,77%)	70,00008 (0,22%)
20	52,64	47	910,05339 (99,77%)	90,00012 (0,22%)
23	52,61	47	900,09989 (99,77%)	100,00022 (0,22%)

Tabela B

Eficiência das unidades,, contribuição daos entradas inputs e referênciase conjunto referência Com Restrição de Multiplicadores – Modelo CCR-I
Observação	Eficiência %	Referência	Contribuição X1	Contribuição X2
194	100,00	-4	810,08658 (80,81%)	190,02056 (19,19%)
194	96,0078,60	194	0,04348 (80,80%)81	0,01033 (20,20%)19
718	92,7260,20	419	780,02608 (79,58%)	220,00619 (20,42%)
212	82,8850,30	419	730,02312 (80,81%)	270,00549 (19,19%)
1210	79,1341,80	419	620,01638 (80,81%)	380,00389 (19,19%)
135	75,6340,20	419	760,02402 (80,79%)	240,00571 (19,21%)
38	75,6038,10	419	640,01758 (80,79%)	360,00418 (19,21%)
1187	74,1634,90	419	730,01869 (80,80%)	270,00444 (19,20%)
714	70,2234,60	419	720,03556 (80,82%)	280,00844 (19,18%)
25	65,8433,30	419	810,02524 (80,82%)	190,00599 (19,18%)
822	64,1429,10	419	810,00458 (80,78%)	190,00109 (19,22%)
1711	63,5527,30	419	810,00557 (80,84%)	190,00132 (19,16%)
156	63,1125,8	419	800,01171 (80,81%)	200,00278 (19,19%)
9	62,7925,6	419	800,00265 (80,79%)	200,00063 (19,21%)
613	61,8825,40	419	810,01549 (80,80%)	190,00368 (19,20%)
1615	61,7325,30	419	720,00867 (80,80%)	280,00206 (19,20%)
112	60,8725,30	419	810,01810 (81,06%)	190,00423 (18,94%)
520	59,2621,30	419	810,00500 (80,77%)	190,00119 (19,23%)
1214	55,7020,70	419	810,00864 (80,82%)	190,00205 (19,18%)
2123	52,5919,70	419	780,00863 (80,80%)	220,00205 (19,20%)
2416	52,4318,10	419	720,00515 (80,85%)	280,00122 (19,15%)
1022	50,4117,60	419	810,00672 (80,87%)	190,00159 (19,13%)
13	50,2917,50	419	710,01194 (80,78%)	290,00284 (19,22%)
2024	49,6115,20	419	810,00629 (80,85%)	190,00149 (19,15%)
231	49,2614,50	419	800,00714 (80,86%)	200,00169 (19,14%)

Bibliografia

Bibliografia

ALLEN R., ATHANASSOPOULOS A., DYSON R G et al., (1997), “Weights Restrictions and Value Judgements in Data Envelopment Analysis: Evolution, Development and Future Directions”, Annals of Operations Research, vol. 73, pp. 13-34.

ARNOLD V, BARDHAN I, COOPER W, KUMBHAKAR S (1996), New uses of DEA and statistical regressions for efficiency evaluation and estimation, Annals of Operations Research 66 , pp 255-277–

BARRODALE I, ROBERTS F D, (1973), An improved algorithm for discrete L₁ linear approximation. S.I.AM., J. Numer. Anal. 10, 839-848

BIRKES D, DODGE Y, (1993) Alternative Methods of Regression. John Wiley and Sons, Inc., New York.

BLATERG R, Sargent T (1971) Regression With Non-Gaussian Stable Disturbances: Some Sampling Results, Eco nometrica, Vol 39, No 3, 501-510

CHARNES A, COOPER W e FERGUSON R, (1955). Optimal estimation of executive compensation by linear programming. Management Science

CHARNES A, COOPER W e RHODES E (1978) Measuring efficiency of Decision making, European Journal of Units Operational Research, 2(6): 429-444.

CHARNES A , COOPER W, WEI Q. L., HUANG Z. M., (1989) “Cone Ratio Data Envelopment Analysis and Multiple Objective Linear Programming”, International Journal of Management Science, Vol.. 20, Nº 7, pp. 1099-1118.

CHARNES A , COOPER W, HUANG Z. M., SUN, D. B., (1990), “Polyhedral Cone-Ratio DEA Models with an illustrative application to Large Commercial Banks”, Journal of Econometrics, Nº 46, pp. 73-91.

Dyson R G, Thanassoulis E., (1988), “Reducing Weight Flexibility in Data Envelopment Analysis”, Journal of the Operational Research Society, v. 39, n. 6, pp. 563-576.

KORNBLUTH, J. S. M., (1991), “Analysing Policy Effectiveness using Cone Restricted DEA”, Journal of the Operational Research Society, Vol. 42, Nº 12, pp. 1097-1104.

MCKEAN J, SCHHRADER R M, (1987), Least absolute errors analysis of variance, Statistical Data Analysis Based on the L₁ – Norm and Related Methods, Elsevier Science Publishers B, 297-305.

MONTGOMERY D C, PECK, (1992) E A, Introduction to Linear Regression Analysis, Wiley & Sons.

NARULA S, WELLINGTON J, (1985), Interior Analysis for the Minimum Sum of Absolute Errors Regression, Technometrics, Vol 27, No 2, 181-188.

NARULA S, (1987) The Minimum sum of absolute errors regression, Journal of Quality Technollogy, 19, 37-45

PEDRAJA-CHAPARRO R., SALINAS-JIMENES J., SMITH P., (1997), “On the Role of Weight Restrictions in DEA”, Journal of Productivity Analysis, Vol. 8, pp. 215-230.

ROLL Y., COOK W., GOLANY B., (1991), “Controlling Factor weights in DEA”, IIE Transactions., Vol. 23, pp. 2-9.

Thompson R G, LANGEMEIER L N, LEE C, LEE, E., THRALL R., (1990), “The Role of Multiplier Bounds in Efficiency Analysis with Application to Kansas Farming”. Journal of Econometrics, v. 46, pp. 93-108.

WONG Y H B, BEASLEY J E, (1990), “Restricting Weight Flexibility in DEA”, Journal of the Operational Research Society, vol. 41, pp. 829-835.

ZHANG Y, (1993) Primal-Dual interior point approach for computing l₁ solutions and l_µ solutions of overdetermined systems, Journal of Optimization Theory and Applications, 77, 323-341

Bibliografia

Bibliografia

Charnes A, Cooper W W e Rhodes E (1978) Measuring efficiency of Decision making, European Journal of Units Operational Research, 2(6): 429-444.

Dyson R G, Thanassoulis E (1988) Reducing weight flexibility in data envelopment analysis Journal of the Operational Research Society 39(6): 563-576.

Wong Y H B, Beasley J E (1990) Restricting Weight Flexibility in Data Envelopment Analysis. Journal of the Operational Research Vol 41, No 9, 829-835.

Charnes A, Cooper W W, Wei Q L e Huang Z M (1989) Cone Ratio data envelopment analysis and multi-objective programming. Int. Journal Syst. Science 20, 1099-1118

Thompson R G, Langemeier L N, Lee C T, Lee E e Thrall R M (1990) The role of multiplier bounds in efficiency analysis with application to Kansas farming. J. Econometric 46, 93-108.

Blaterg R, Sargent T (1971) Regression With Non-Gaussian Stable Disturbances: Some Sampling Results, Econometrica, Vol 39, No 3, 501-510

Montgomery D C, Peck E A, Introduction to Linear Regression Analysis, Wiley & Sons. (1992)

Charnes, A, Cooper W e Ferguson R, (1955). Optimal estimation of executive compensation by linear programming. Management Science

Barrodale, I, Roberts F D, (1973), An improved algorithm for discrete L₁ linear approximation. S.I.AM., J. Numer. Anal. 10, 839-848

Zhang, Y, (1993) Primal-Dual interior point approach for computing l₁ solutions and l_µ solutions of overdetermined systems, Journal of Optimization Theory and Applications, 77, 323-341

Narula S, Wellington J, Interior Analysis for the Minimum Sum of Absolute Errors Regression, Technometrics, Vol 27, No 2, 181-188.

Narula S, (1987) The Minimum sum of absolute errors regression, Journal of Quality Technollogy, 19, 37-45

Birkes D, Dodge Y, (1993) Alternative Methods of Regression. John Wiley and Sons, Inc., New York.

Mckean J, Schhrader R M, (1987), Least absolute errors analysis of variance, Statistical Data Analysis Based on the L₁ – Norm and Related Methods, Elsevier Science Publishers B, 297-305.

ALLEN, R., ATHANASSOPOULOS, A., DYSON, R. G. et al., 1997, “Weights Restrictions and Value Judgements in Data Envelopment Analysis: Evolution, Development and Future Directions”, Annals of Operations Research, vol. 73, pp. 13-34.

CHARNES, A , COOPER, W. W., WEI, Q. L., HUANG, Z. M., 1989, “Cone Ratio Data Envelopment Analysis and Multiple Objective Linear Programming”, International Journal of Management Science, Vol.. 20, Nº 7, pp. 1099-1118.

CHARNES, A , COOPER, W. W., HUANG, Z. M., SUN, D. B., 1990, “Polyhedral Cone-Ratio DEA Models with an illustrative application to Large Commercial Banks”, Journal of Econometrics, Nº 46, pp. 73-91.

Dyson, R. G., Thanassoulis, E., 1988, “Reducing Weight Flexibility in Data Envelopment Analysis”, Journal of the Operational Research Society, v. 39, n. 6, pp. 563-576.

KORNBLUTH, J. S. M., 1991, “Analysing Policy Effectiveness using Cone Restricted DEA”, Journal of the Operational Research Society, Vol. 42, Nº 12, pp. 1097-1104.

PEDRAJA-CHAPARRO, R., SALINAS-JIMENES, J., SMITH, P., 1997, “On the Role of Weight Restrictions in DEA”, Journal of Productivity Analysis, Vol. 8, pp. 215-230.

ROLL, Y., COOK, W., GOLANY, B., 1991, “Controlling Factor weights in DEA”, IIE Transactions., Vol. 23, pp. 2-9.

Thompson, R. G., LANGEMEIER, L. N., LEE, C., LEE, E., THRALL, R., 1990, “The Role of Multiplier Bounds in Efficiency Analysis with Application to Kansas Farming”. Journal of Econometrics, v. 46, pp. 93-108.

WONG, Y.-H. B., BEASLEY, J. E., 1990, “Restricting Weight Flexibility in DEA”, Journal of the Operational Research Society, vol. 41, pp. 829-835.